
【题目】已知圆O经过椭圆C:![]() =1(a>b>0)的两个焦点以及两个顶点,且点(b,
=1(a>b>0)的两个焦点以及两个顶点,且点(b,![]() )在椭圆C上.
)在椭圆C上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l与圆O相切,与椭圆C交于M、N两点,且|MN|=![]() ,求直线l的倾斜角.
,求直线l的倾斜角.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)先由题意得出![]() ,可得出
,可得出![]() 与
与![]() 的等量关系,然后将点的坐标代入椭圆
的等量关系,然后将点的坐标代入椭圆![]() 的方程,可求出
的方程,可求出![]() 与
与![]() 的值,从而得出椭圆
的值,从而得出椭圆![]() 的方程;(2)对直线
的方程;(2)对直线![]() 的斜率是否存在进行分类讨论,当直线
的斜率是否存在进行分类讨论,当直线![]() 的斜率不存在时,可求出
的斜率不存在时,可求出![]() ,然后进行检验;当直线
,然后进行检验;当直线![]() 的斜率存在时,可设直线
的斜率存在时,可设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() ,先由直线
,先由直线![]() 与圆
与圆![]() 相切得出
相切得出![]() 与
与![]() 之间的关系,再将直线
之间的关系,再将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立,由韦达定理,利用弦长公式并结合条件
的方程联立,由韦达定理,利用弦长公式并结合条件![]() 得出
得出![]() 的值,从而求出直线
的值,从而求出直线![]() 的倾斜角.
的倾斜角.
(1)由题可知圆![]() 只能经过椭圆的上下顶点,所以椭圆焦距等于短轴长,可得
只能经过椭圆的上下顶点,所以椭圆焦距等于短轴长,可得![]() ,
,
又点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,解得
,解得![]() ,
,
即椭圆![]() 的方程为
的方程为![]() .
.
(2)圆![]() 的方程为
的方程为![]() ,当直线
,当直线![]() 不存在斜率时,解得
不存在斜率时,解得![]() ,不符合题意;
,不符合题意;
当直线![]() 存在斜率时,设其方程为
存在斜率时,设其方程为![]() ,因为直线
,因为直线![]() 与圆
与圆![]() 相切,所以
相切,所以![]() ,即
,即![]() .
.
将直线![]() 与椭圆
与椭圆![]() 的方程联立,得:
的方程联立,得:
![]() ,
,
判别式![]() ,即
,即![]() ,
,
设![]() ,则
,则![]()
![]() ,
,
所以![]() ,
,
解得![]() ,
,
所以直线![]() 的倾斜角为
的倾斜角为![]() 或
或![]() .
.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.首届中国国际进口博览会的某展馆棚顶一角的钢结构可以抽象为空间图形阳马.如图所示,在阳马![]() 中,
中,![]() 底面
底面![]() .
.
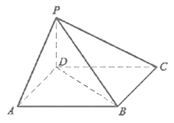
(1)若![]() ,斜梁
,斜梁![]() 与底面
与底面![]() 所成角为
所成角为![]() ,求立柱
,求立柱![]() 的长(精确到
的长(精确到![]() );
);
(2)证明:四面体![]() 为鳖臑;
为鳖臑;
(3)若![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一个动点,求
上一个动点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-ax-alnx(a∈R).
(1)若函数f(x)在x=1处取得极值,求a的值;
(2)在(1)的条件下,求证:f(x)≥-![]() +
+![]() -4x+
-4x+![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一![]() 班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.

![]() 1
1![]() 求分数在
求分数在![]() 的频数及全班人数;
的频数及全班人数;
![]() 2
2![]() 求分数在
求分数在![]() 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中![]() 间矩形的高;
间矩形的高;
![]() 3
3![]() 若要从分数在
若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 上一点
上一点![]() 到焦点的距离为4,动直线
到焦点的距离为4,动直线![]() 交抛物线
交抛物线![]() 于坐标原点O和点A,交抛物线
于坐标原点O和点A,交抛物线![]() 的准线于点B,若动点P满足
的准线于点B,若动点P满足![]() ,动点P的轨迹C的方程为
,动点P的轨迹C的方程为![]() .
.
(1)求出抛物线![]() 的标准方程;
的标准方程;
(2)求动点P的轨迹方程![]() ;
;
(3)以下给出曲线C的四个方面的性质,请你选择其中的三个方面进行研究:①对称性;②范围;③渐近线;④![]() 时,写出由
时,写出由![]() 确定的函数
确定的函数![]() 的单调区间.
的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() 的棱长为4,E、F分别是棱AB、
的棱长为4,E、F分别是棱AB、![]() 的中点,联结EF、
的中点,联结EF、![]() 、
、![]() 、
、![]() E、
E、![]() E、
E、![]() E.
E.

![]() 求三棱锥
求三棱锥![]() 的体积;
的体积;
![]() 求直线
求直线![]() 与平面
与平面![]() 所成角的大小
所成角的大小![]() 结果用反三角函数值表示
结果用反三角函数值表示![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的各项均不为零.设数列
的各项均不为零.设数列![]() 的前n项和为Sn,数列
的前n项和为Sn,数列![]() 的前n项和为Tn, 且
的前n项和为Tn, 且![]()
![]() .
.
(1)求![]() 的值;
的值;
(2)证明:数列![]() 是等比数列;
是等比数列;
(3)若![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的所有值.
的所有值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com