
已知x,y满足约束条件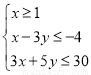
(1)求目标函数z=2x-y的最大值和最小值;
(2)若目标函数z=ax+y取得最大值的最优解有无穷多个,求a的值;
(3)求z=x2+y2的取值范围.
(1)zmax=2×5-3=7,zmin=2×1-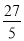 =-
=-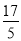 .
.
(2)a=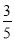 .
.
(3)[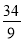 ,34]
,34]
【解析】【解析】
(1)作出不等式组表示的可行域如图:
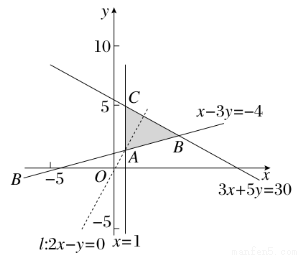
作直线l:2x-y=0,并平行移动使它过可行域内的B点,此时z有最大值;过可行域内的C点,此时z有最小值,
解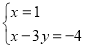 ,得A(1,
,得A(1,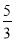 ).
).
解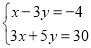 ,得B(5,3).
,得B(5,3).
解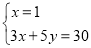 ,得C(1,
,得C(1,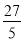 ).
).
∴zmax=2×5-3=7,zmin=2×1-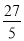 =-
=-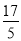 .
.
(2)一般情况下,当z取得最大值时,直线所经过的点都是唯一的,但若直线平行于边界直线,即直线z=ax+y平行于直线3x+5y=30时,线段BC上的任意一点均使z取得最大值,此时满足条件的点即最优解,有无数个.
又kBC=-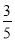 ,∴-a=-
,∴-a=-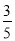 ,∴a=
,∴a=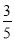 .
.
(3)z=x2+y2,则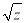 为(x,y)与原点(0,0)的距离,结合不等式的区域,易知A点到原点距离最小为
为(x,y)与原点(0,0)的距离,结合不等式的区域,易知A点到原点距离最小为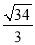 ,最大值为|OB|、|OC|、原点O到直线3x+5y=30距离三者之一,计算得,最大值为|OB|=
,最大值为|OB|、|OC|、原点O到直线3x+5y=30距离三者之一,计算得,最大值为|OB|=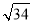 .故z=x2+y2的取值范围是[
.故z=x2+y2的取值范围是[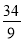 ,34].
,34].


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-1分类加法与分步乘法计数原理(解析版) 题型:填空题
某县从10名大学毕业的选调生中选3个人担任镇长助理,则甲、乙至少有1人入选,而丙没有入选的不同选法的种数为( )
A.85 B.56 C.49 D.28
查看答案和解析>>
科目:高中数学 来源:2015高考数学理配套特训:10-9离散型随机变量均值方差和正态分布(解析版) 题型:解答题
某示范性高中的校长推荐甲、乙、丙三名学生参加某大学自主招生考核测试,在本次考核中只有合格和优秀两个等级.若考核为合格,授予10分降分资格;考核为优秀, 授予20分降分资格.假设甲、乙、丙考核为优秀的概率分别为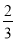 、
、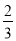 、
、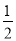 ,他们考核所得的等级相互独立.
,他们考核所得的等级相互独立.
(1)求在这次考核中,甲、乙、丙三名学生至少有一名考核为优秀的概率;
(2)记在这次考核中甲、乙、丙三名学生所得降分之和为随机变量ξ,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2015高考数学理一轮配套特训:7-1空间几何体结构及三视图和直观图(解析版) 题型:填空题
如图,一个封闭的三棱柱容器中盛有水,且侧棱长AA1=8.若侧面AA1B1B水平放置时,液面恰好经过AC,BC,A1C1,B1C1的中点. 当底面ABC水平放置时,液面高度为________.
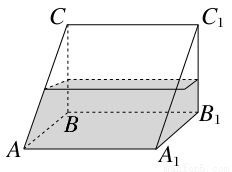
查看答案和解析>>
科目:高中数学 来源:2015高考数学理一轮配套特训:7-1空间几何体结构及三视图和直观图(解析版) 题型:选择题
下列四个几何体中,每个几何体的三视图中有且仅有两个视图相同的是( )

A.①② B.①③ C.③④ D.②④
查看答案和解析>>
科目:高中数学 来源:2015高考数学理一轮配套特训:6-3二元一次不等式及简单的线性规划(解析版) 题型:填空题
已知实数x,y满足 ,若目标函数z=ax+y(a≠0)取得最小值时的最优解有无数个,则实数a的值为________.
,若目标函数z=ax+y(a≠0)取得最小值时的最优解有无数个,则实数a的值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学理一轮配套特训:3-2同角三角函数基本关系式与诱导公式(解析版) 题型:解答题
是否存在α∈(-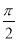 ,
,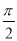 ),β∈(0,π),使等式sin(3π-α)=
),β∈(0,π),使等式sin(3π-α)=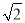 cos(
cos(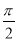 -β),
-β), cos(-α)=-
cos(-α)=-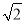 cos(π+β)同时成立?若存在,求出α,β的值;若不存在,请说明理由.
cos(π+β)同时成立?若存在,求出α,β的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015高考数学理一轮配套特训:3-1任意角弧度制及任意角的三角函数(解析版) 题型:解答题
已知角α终边经过点P(x,-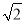 )(x≠0),且cosα=
)(x≠0),且cosα=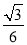 x,求sinα、tanα的值.
x,求sinα、tanα的值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学一轮配套特训:1-2命题及其关系、充分条件与必要条件(解析版) 题型:选择题
“10a>10b”是“lga>lgb”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com