科目：高中数学 来源： 题型：解答题
(本小题满分12分) 已知函数f(x)＝
(1)作出函数
的图像简图，并指出函数的单调区间；
（2）若f(2－a2)>f(a)，求实数a的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本题满分10分） 如图，有一块矩形空地，要在这块空地上辟一个内接四边形为绿地，使其四个顶点分别落在矩形的四条边上，已知AB＝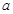
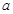（>2），BC＝2，且AE＝AH＝CF＝CG，
设AE＝
，绿地面积为
.
（1）写出关于的函数关系式，并指出这个函数的定义域;
（2）当AE为何值时，绿地面积最大？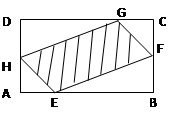
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本小题满分14分）如图，建立平面直角坐标系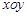
，
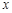轴在地平面上，
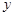轴垂直于地
平面，单位长度为1千米，某炮位于坐标原点．已知炮弹发射后的轨迹在方程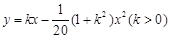
表示的曲线上，其中
与发射方向有关，炮的射程是指炮弹落地点的横坐标．
（1）求炮的最大射程；
（2）设在第一象限有一飞行物（忽略其大小），其飞行高度为3.2千米，试问它的横坐标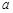
不超过多少时，炮弹可以击中它？请说明理由．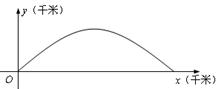
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
某品牌电视生产厂家有A、B两种型号的电视机参加了家电下乡活动，若厂家A、B对两种型号的电视机的投放金额分别为p、q万元，农民购买电视机获得的补贴分别为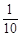
p、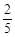
lnq万元，已知A、B两种型号的电视机的投放总额为10万元，且A、B两种型号的电视机的投放金额均不低于1万元，请你制定一个投放方案，使得在这次活动中农民得到的补贴最多，并求出最大值(精确到0.1，参考数据：
)．
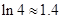查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
.(2) 
.
是奇函数. 
的值；
在区间
上单调递增，求实数
的取值范围. 
为奇函数，
为常数。
在区间
内单调递增；
上的每一个
的值，不等式
恒成立，求实数
的取值范围。
是定义在
上的减函数，并且满足
，
,
,
的值，（2）如果
，求x的取值范围。
且对任意实数
均有
成立，求
表达式；
时，
是单调函数，求实数
的取值范围。