练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    .已知函数 是奇函数.
    （1）求实数的值；
    （2）若函数在区间上单调递增，求实数的取值范围.

    （1）。（2）∴

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    已知26辆货车以相同速度v由A地驶向400千米处的B地，每两辆货车间距离为d千米，现已知d与v的平方成正比，且当v=20（千米／时）时，d=1（千米）．
    （1）写出d与v的函数关系；
    （2）若不计货车的长度，则26辆货车都到达B地最少需要多少小时？此时货车速度是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    (本小题满分12分)
    已知二次函数，，的最小值为．
    ⑴ 求函数的解析式；
    ⑵ 设，若在上是减函数，求实数的取值范围；

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本题满分14分）
    已知函数的图象经过点和，记（）
    （1）求数列的通项公式；
    （2）设，若，求的最小值；
    （3）求使不等式对一切均成立的最大实数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分14分）
    某漁业公司年初用98万元购买一艘捕魚船，第一年各种支出费用12万元，以后每年都增加
    4万元，每年捕魚收益50万元．
    （1）该公司第几年开始获利？
    （2）若干年后，有两种处理方案：
    ①年平均获利最大时，以26万元出售该渔船；
    ②总纯收入获利最大时，以8万元出售渔船．
    问哪种处理方案最合算?

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    (本题满分12分)二次函数f(x)的最小值为1，且f(0)＝f(2)＝3.
    (1)求f(x)的解析式；(2)若f(x)在区间[2a，a＋1]上不单调，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （1）
    (2)求值

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    .计算（1） （2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

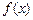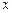    某公司生产陶瓷，根据历年的情况可知，生产陶瓷每天的固定成本为14000元，每生产一件产品，成本增加210元．已知该产品的日销售量与产量之间的关系式为
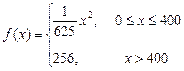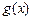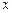    ，每件产品的售价与产量之间的关系式为
    ．
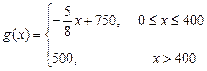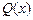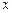    （Ⅰ）写出该陶瓷厂的日销售利润与产量之间的关系式；
    （Ⅱ）若要使得日销售利润最大，每天该生产多少件产品，并求出最大利润．

    查看答案和解析>>

    同步练习册答案