
(本题满分10分) 如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=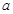 (
(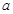 >2),BC=2,且AE=AH=CF=CG,
>2),BC=2,且AE=AH=CF=CG,
设AE= ,绿地面积为
,绿地面积为 .
.
(1)写出 关于
关于 的函数关系式,并指出这个函数的定义域;
的函数关系式,并指出这个函数的定义域;
(2)当AE为何值时,绿地面积 最大?
最大?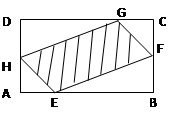
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
已知集合M是满足下列性质的函数f(x)的全体:存在非零常数T,对任意x∈R,有f(x+T)="T" f(x)成立.
(Ⅰ)函数f(x)=" x" 是否属于集合M?说明理由;
(Ⅱ)设函数f(x)=ax(a>0,且a≠1)的图象与y=x的图象有公共点,证明:f(x)=ax∈M;
(Ⅲ)若函数f(x)=sinkx∈M ,求实数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度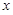 (单位:cm)满足关系:
(单位:cm)满足关系: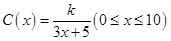 ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设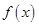 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(Ⅰ)求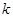 的值及
的值及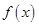 的表达式;
的表达式;
(Ⅱ)隔热层修建多厚时,总费用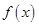 达到最小,并求最小值.
达到最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
某漁业公司年初用98万元购买一艘捕魚船,第一年各种支出费用12万元,以后每年都增加
4万元,每年捕魚收益50万元.
(1)该公司第几年开始获利?
(2)若干年后,有两种处理方案:
①年平均获利最大时,以26万元出售该渔船;
②总纯收入获利最大时,以8万元出售渔船.
问哪种处理方案最合算?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车
流速度v(单位:千米/小时)是车流密度 x(单位:辆/千米)的函数.当桥上的车流密度达
到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速
度为60千米/小时.研究表明当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值.(精确到1辆/小时)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com