
如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|= ,|AF2|=
,|AF2|=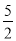 .
.
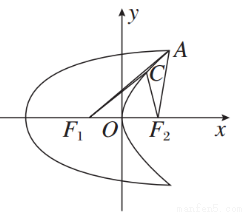
(1)求曲线C1和C2的方程;
(2)设点C是C2上一点,若|CF1|=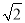 |CF2|,求△CF1F2的面积.
|CF2|,求△CF1F2的面积.
(1)曲线C1的方程为 +
+ =1(-3≤x≤
=1(-3≤x≤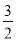 ),曲线C2的方程为y2=4x(0≤x≤
),曲线C2的方程为y2=4x(0≤x≤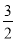 )
)
(2)2
【解析】(1)设椭圆方程为 +
+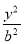 =1(a>b>0),则2a=|AF1|+|AF2|=
=1(a>b>0),则2a=|AF1|+|AF2|=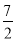 +
+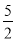 =6,得a=3.
=6,得a=3.
设A(x,y),F1(-c,0),F2(c,0),则(x+c)2+y2=( )2,(x-c)2+y2=(
)2,(x-c)2+y2=(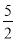 )2,两式相减得xc=
)2,两式相减得xc=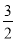 .由抛物线的定义可知|AF2|=x+c=
.由抛物线的定义可知|AF2|=x+c= ,
,
则c=1,x=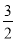 或x=1,c=
或x=1,c= .又∠AF2F1为钝角,
.又∠AF2F1为钝角,
则x=1,c= 不合题意,舍去.当c=1时,b=2
不合题意,舍去.当c=1时,b=2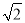 ,
,
所以曲线C1的方程为 +
+ =1(-3≤x≤
=1(-3≤x≤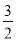 ),曲线C2的方程为y2=4x(0≤x≤
),曲线C2的方程为y2=4x(0≤x≤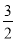 ).
).
(2)过点F1作直线l垂直于x轴,过点C作CC1⊥l于点C1,依题意知|CC1|=|CF2|.
在Rt△CC1F1中,|CF1|=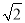 |CF2|=
|CF2|=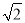 |CC1|,所以∠C1CF1=45°,
|CC1|,所以∠C1CF1=45°,
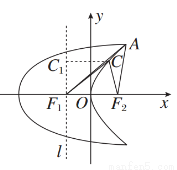
所以∠CF1F2=∠C1CF1=45°.
在△CF1F2中,设|CF2|=r,则|CF1|=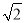 r,|F1F2|=2.
r,|F1F2|=2.
由余弦定理得22+(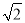 r)2-2×2×
r)2-2×2×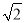 rcos45°=r2,
rcos45°=r2,
解得r=2,
所以△CF1F2的面积S△CF1F2=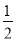 |F1F2|·|CF1|sin45°=
|F1F2|·|CF1|sin45°=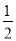 ×2×2
×2×2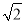 sin45°=2.
sin45°=2.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:选4-1-1相似三角形判定及性质(解析版) 题型:解答题
如图所示,已知,在边长为1的正方形ABCD的一边上取一点E,使AE=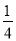 AD,从AB的中点F作HF⊥EC于H.
AD,从AB的中点F作HF⊥EC于H.
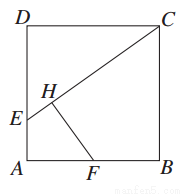
(1)求证:FH=FA;
(2)求EH∶HC的值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:9-1随机抽样(解析版) 题型:填空题
一个总体中的1000个个体编号为0,1,2,…,999,并依次将其分为10个小组,组号为0,1,2,…,9,要用系统抽样的方法抽取一个容量为10的样本,规定若在第0组随机抽取的号码为x,则第k组中抽取的号码的后两位数为x+33k的后两位数.当x=24时,所抽取样本的10个号码是________,若所抽取样本的10个号码中有一个的后两位数是87,则x的取值集合是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-9圆锥曲线的综合问题(解析版) 题型:解答题
椭圆C的中心在原点,焦点在x轴上,两焦点F1,F2之间的距离为2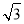 ,椭圆上第一象限内的点P满足PF1⊥PF2,且△PF1F2的面积为1.
,椭圆上第一象限内的点P满足PF1⊥PF2,且△PF1F2的面积为1.
(1)求椭圆C的标准方程;
(2)若椭圆C的右顶点为A,直线l:y=kx+m(k≠0)与椭圆C交于不同的两点M,N,且满足AM⊥AN.求证:直线l过定点,并求出定点的坐标.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-9圆锥曲线的综合问题(解析版) 题型:选择题
若双曲线 -
- =1(a>0,b>0)上不存在点P,使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,则该双曲线离心率的取值范围为( )
=1(a>0,b>0)上不存在点P,使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,则该双曲线离心率的取值范围为( )
A.(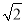 ,+∞) B.[
,+∞) B.[ ,+∞)
,+∞)
C.(1, ] D.(1,
] D.(1, )
)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-8曲线与方程(解析版) 题型:解答题
已知点C(1,0),点A、B是⊙O:x2+y2=9上任意两个不同的点,且满足 ·
·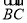 =0,设P为弦AB的中点.
=0,设P为弦AB的中点.
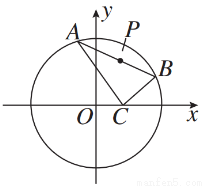
(1)求点P的轨迹T的方程;
(2)试探究在轨迹T上是否存在这样的点:它到直线x=-1的距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-8曲线与方程(解析版) 题型:选择题
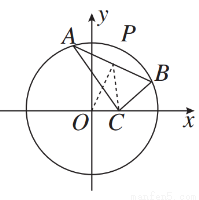
设圆(x+1)2+y2=25的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点.线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为( )
A. -
- =1 B.
=1 B. +
+ =1
=1
C.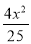 -
- =1 D.
=1 D. +
+ =1
=1
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-7抛物线(解析版) 题型:选择题
已知F是抛物线y2=x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到y轴的距离为( )
A.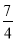 B.
B.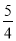 C.
C. D.1
D.1
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-4直线与圆、圆与圆的位置关系(解析版) 题型:填空题
已知直线l:x-y+4=0与圆C:(x-1)2+(y-1)2=2,则圆C上各点到l距离的最小值为________,最大值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com