
椭圆C的中心在原点,焦点在x轴上,两焦点F1,F2之间的距离为2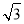 ,椭圆上第一象限内的点P满足PF1⊥PF2,且△PF1F2的面积为1.
,椭圆上第一象限内的点P满足PF1⊥PF2,且△PF1F2的面积为1.
(1)求椭圆C的标准方程;
(2)若椭圆C的右顶点为A,直线l:y=kx+m(k≠0)与椭圆C交于不同的两点M,N,且满足AM⊥AN.求证:直线l过定点,并求出定点的坐标.
(1) +y2=1 (2)见解析
+y2=1 (2)见解析
【解析】(1)设椭圆的标准方程为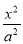 +
+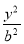 =1(a>b>0),因为|F1F2|=2
=1(a>b>0),因为|F1F2|=2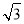 ,所以c=
,所以c=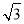 ,由S△PF1F2=1,得|PF1||PF2|=2,又由PF1⊥PF2,得|PF1|2+|PF2|2=|F1F2|2=12,即(|PF1|+|PF2|)2-2|PF1||PF2|=12,即4a2-4=12,a2=4,b2=a2-3=1,所以椭圆C的标准方程为
,由S△PF1F2=1,得|PF1||PF2|=2,又由PF1⊥PF2,得|PF1|2+|PF2|2=|F1F2|2=12,即(|PF1|+|PF2|)2-2|PF1||PF2|=12,即4a2-4=12,a2=4,b2=a2-3=1,所以椭圆C的标准方程为 +y2=1.
+y2=1.
(2)由方程组 ,得(1+4k2)x2+8kmx+4m2-4=0,
,得(1+4k2)x2+8kmx+4m2-4=0,
Δ=(8km)2-4(1+4k2)(4m2-4)>0,整理得4k2-m2+1>0.
设M(x1,y1),N(x2,y2),则x1+x2=-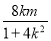 ,x1x2=
,x1x2= .
.
由AM⊥AN且椭圆的右顶点为A(2,0),得(x1-2)(x2-2)+y1y2=0,
因为y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2,
所以(1+k2)x1x2+(km-2)(x1+x2)+m2+4=0,
即(1+k2)·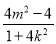 +(km-2)·
+(km-2)· +m2+4=0,
+m2+4=0,
整理得:5m2+16mk+12k2=0,
解得m=-2k或m=-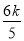 ,均满足4k2-m2+1>0.
,均满足4k2-m2+1>0.
当m=-2k时,直线的l方程为y=kx-2k,过定点(2,0),与题意矛盾,舍去;
当m=-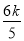 时,直线l的方程为y=k(x-
时,直线l的方程为y=k(x-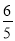 ),过定点(
),过定点( ,0),符合题意.
,0),符合题意.
故直线l过定点,且定点的坐标为(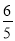 ,0).
,0).


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:选4-1-2直线与圆的位置关系(解析版) 题型:填空题
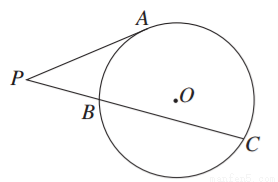
如图,PA是圆O的切线,A为切点,PBC是圆O的割线.若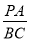 =
=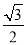 ,则
,则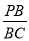 =________.
=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:9-2用样本估计总体(解析版) 题型:解答题
某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30 min抽取一包产品,称其重量,分别记录抽查数据如下:
甲:102,101,99,98,103,98,99;
乙:110,115,90,85,75,115,110.
(1)这种抽样方法是哪一种?
(2)将这两组数据用茎叶图表示;
(3)将两组数据比较,说明哪个车间的产品较稳定.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:9-1随机抽样(解析版) 题型:填空题
某公路设计院有工程师6人,技术员12人,技工18人,要从这些人中抽取n个人参加市里召开的科学技术大会.如果采用系统抽样和分层抽样的方法抽取,不用剔除个体,如果参会人数增加1个,则在采用系统抽样时,需要在总体中先剔除1个个体,则n=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:9-1随机抽样(解析版) 题型:选择题
某单位有职工52人,现将所有职工随机编号,用系统抽样的方法抽取一个容量为4的样本,已知6号,32号,45号职工在样本中,则样本中另外一个职工的编号是( )
A.19 B.20 C.18 D.21
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-9圆锥曲线的综合问题(解析版) 题型:填空题
椭圆x2+ky2=1的一个焦点是(0,2),则k的值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-8曲线与方程(解析版) 题型:解答题
如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|= ,|AF2|=
,|AF2|=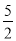 .
.
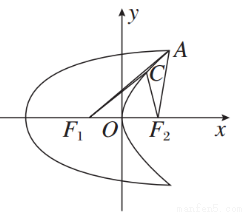
(1)求曲线C1和C2的方程;
(2)设点C是C2上一点,若|CF1|=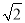 |CF2|,求△CF1F2的面积.
|CF2|,求△CF1F2的面积.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-7抛物线(解析版) 题型:填空题
过抛物线y2=2px(p>0)的焦点F作倾斜角为45°的直线交抛物线于A,B两点,若线段AB的长为8,则p=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-5椭圆(解析版) 题型:选择题
椭圆 +
+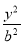 =1(a>b>0)的左顶点为A,左、右焦点分别为F1,F2,D是它短轴上的一个端点,若3
=1(a>b>0)的左顶点为A,左、右焦点分别为F1,F2,D是它短轴上的一个端点,若3 =
=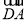 +2
+2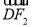 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )
A.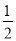 B.
B.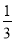 C.
C.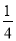 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com