
如图所示,已知,在边长为1的正方形ABCD的一边上取一点E,使AE=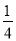 AD,从AB的中点F作HF⊥EC于H.
AD,从AB的中点F作HF⊥EC于H.
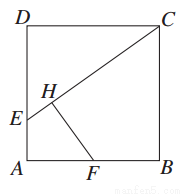
(1)求证:FH=FA;
(2)求EH∶HC的值.
(1)见解析 (2)1∶4
【解析】【解析】
(1)证明:连接EF,FC,在正方形ABCD中,AD=AB=BC,∠A=∠B=90°.
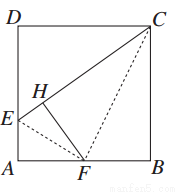
∵AE=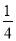 AD,F为AB的中点,
AD,F为AB的中点,
∴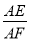 =
=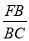 .
.
∴△EAF∽△FBC,
∴∠AEF=∠BFC,∠EFA=∠BCF.
又∠A=∠B=90°,
∴∠EFC=90°,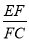 =
=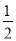 .
.
又∵∠EFC=∠B=90°,∴△EFC∽△FBC.
∴∠HEF=∠BFC,∠ECF=∠BCF.
∴∠AEF=∠HEF,∠AFE=∠HFE,又EF=EF,
∴△EAF≌△EHF,∴FH=FA.
(2)由(1)知△EFC是直角三角形,FH是斜边EC上的高,
由射影定理可得EF2=EH·EC,FC2=CH·CE,于是EH∶HC=EF2∶FC2.
由(1)得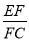 =
=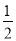 ,于是EH∶HC=EF2∶FC2=1∶4.
,于是EH∶HC=EF2∶FC2=1∶4.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:选4-1-2直线与圆的位置关系(解析版) 题型:填空题
如图,PA是圆O的切线,A为切点,PBC是圆O的割线.若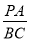 =
=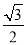 ,则
,则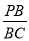 =________.
=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:选4-1-2直线与圆的位置关系(解析版) 题型:选择题
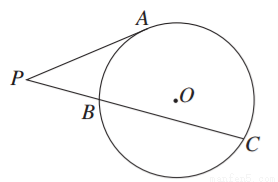
如图,∠ACB=90°,CD⊥AB于点D,以BD为直径的圆与BC交于点E,则( )
A.CE·CB=AD·DB B.CE·CB=AD·AB
C.AD·AB=CD2 D.CE·EB=CD2
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:选4-1-1相似三角形判定及性质(解析版) 题型:填空题
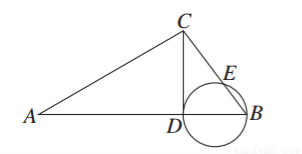
已知梯形ABCD的上底AD=8 cm,下底BC=15 cm,在边AB、CD上分别取E、F,使AE∶EB=DF∶FC=3∶2,则EF=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:9-4算法初步(解析版) 题型:解答题
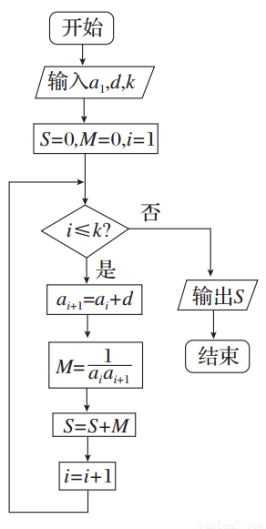
已知数列{an}的各项均为正数,观察如图所示的程序框图,若k=5,k=10时,分别有S=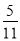 和S=
和S=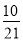 ,求数列{an}的通项公式.
,求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:9-2用样本估计总体(解析版) 题型:解答题
某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30 min抽取一包产品,称其重量,分别记录抽查数据如下:
甲:102,101,99,98,103,98,99;
乙:110,115,90,85,75,115,110.
(1)这种抽样方法是哪一种?
(2)将这两组数据用茎叶图表示;
(3)将两组数据比较,说明哪个车间的产品较稳定.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-8曲线与方程(解析版) 题型:解答题
如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|= ,|AF2|=
,|AF2|=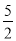 .
.
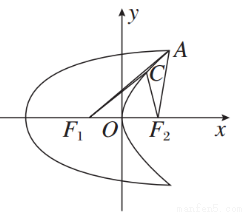
(1)求曲线C1和C2的方程;
(2)设点C是C2上一点,若|CF1|=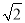 |CF2|,求△CF1F2的面积.
|CF2|,求△CF1F2的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com