如图10-22，在正三棱柱ABC—A1B1C1中，AB=3，AA1=4，M为AA1的中点，P是BC上一点，且由P沿棱柱侧面经过棱CC1到M的最短路线长为
，设这条最短路线与CC1的交点为N。
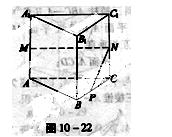
求：（1）该三棱柱侧面展开图的对角线长；
（2）PC与NC的长；
（3）平面NMP与平面ABC所成二面角（锐角）的大小（用反三角函数表示）。
同步练习强化拓展系列答案科目：高中数学 来源： 题型：
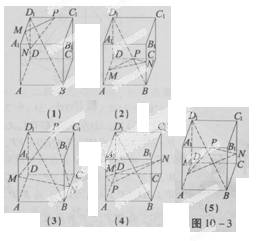
下列五个正方体图形中，l是正方体的一条对角线，点M、N、P分别为其所在棱的中点，能得出l⊥面MNP的图形的序号是_________.(写出所有符合要求的图形序号)
查看答案和解析>>
科目：高中数学 来源： 题型：
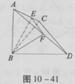
如图，正三棱柱ABC—A1B1C1底面边长为a，侧棱长为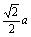
，D是A1C1的中点。
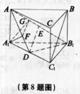
（1）求证：BC1∥平面B1DA；
（2）求证：平面AB1D⊥平面A1ACC1；
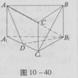
（3）求二面角A1—AB1—D的大小。
查看答案和解析>>
科目：高中数学 来源： 题型：
如图11-18，直二面角D-AB-E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点且BF⊥平面ACE。
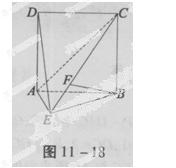
（1）求证：AE⊥平面BCE；
（2）求二面角B-AC-E的大小；
（3）求点D到平面ACE的距离。
查看答案和解析>>
科目：高中数学 来源： 题型：
高三(1)班共有56人
，学号依次为1,2,3，…，56，现用系统抽样的办法抽取一个容量为4的样本．已知学号为6,34,48的同学在样本中，那么还有一个同学的学号应为_____
___．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
角）。在Rt△PHC中，∵∠PCH=
∠PCP1=60°，∴CH=
、在Rt△NCH中tan∠NHC=
∠NHC=arctan
∴平面NMP与平面ABC所成二面角（锐角）的大小为arctan
.故平面NMP与平面ABC所成二面角（锐角）的大小为arccos
.
=___________。
则
的最大值是______.
，圆心在直线
上，圆被直线
截得的弦长为
，则圆的标准方程为 
是两条不同直线，
是三个不同平面，下列命题中正确的是（ ）
B．
D．