练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．复数z满足z（4+i）=3+i，则复数z在复平面内对应的点位于（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    分析 把已知等式变形，利用复数代数形式的乘除运算化简，求出z的坐标得答案．

    解答 解：由z（4+i）=3+i，得
    $z=\frac{3+i}{4+i}=\frac{（3+i）（4-i）}{（4+i）（4-i）}=\frac{13+i}{17}=\frac{13}{17}+\frac{1}{17}i$，
    ∴复数z在复平面内对应的点的坐标为（$\frac{13}{17}，\frac{1}{17}$），位于第一象限．
    故选：A．

    点评 本题考查复数的代数表示法及其几何意义，是基础题的计算题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    17．函数$y=sin（{\frac{π}{6}-x}）$，$x∈[{0，\frac{3π}{2}}]$的单调递减区间是$[{0，\frac{2}{3}π}]$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．对于实数a＞0，“$\frac{1}{x}$＜a”是“x＞$\frac{1}{a}$”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

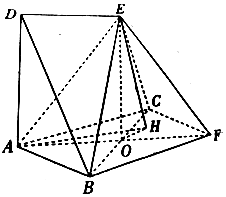    1．如图，边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直，AF∩BC=O，DE=$\sqrt{2}$，ED∥AF且∠DAF=90°
    （1）求证：DE⊥平面BCE
    （2）过O作OH⊥平面BEF，垂足为H，求二面角H-AE-O的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=mlnx+（m-1）x（m∈R）．
    （Ⅰ）当m=3时，求曲线y=f（x）在点（1，f（1））处的切线方程；
    （Ⅱ）若f（x）存在最大值M，且M＞0，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知圆O：x2+y2=1，点P为直线x-2y-3=0上一动点，过点P向圆O引两条切线PA，PB，A、B为切点，则直线AB经过定点（　　）
    A．（2，0）B．（3，0）C．（$\frac{1}{2}$，-1）D．（$\frac{1}{3}$，-$\frac{2}{3}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知k∈R，点P（a，b）是直线x+y=2k与圆x2+y2=k2-2k+3的公共点，则ab的最大值为（　　）
    A．15B．9C．1D．-$\frac{5}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知f（x）是定义在（0，+∞）上的单调函数，且?x∈（0，+∞），f[f（x）-lnx]=e+1，设a=f（（$\frac{1}{2}$）${\;}^{\frac{1}{3}}$），b=f（（$\frac{1}{3}$）${\;}^{\frac{1}{2}}$），c=f（log2π），则a，b，c的大小关系是c＞a＞b（用“＞”号连接表示）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．如表示意某科技公司2012～2016年年利润y（单位：十万元）与年份代号x之间的关系，如果该公司盈利变化规律保持不变，则第n年（以2012年为第1年）年利润的预报值是y=2n2-n．（直接写出代数式即可，不必附加单位）
    年份20122013201420152016
    年份代号x12345
    年利润/十万元16152845

    查看答案和解析>>

    同步练习册答案