
| 资金投入x | 2 | 3 | 4 | 5 | 6 |
| 利润y | 2 | 3 | 5 | 6 | 9 |
 |
| y |
 |
| e |
 |
| ei |
 |
| yi |
. |
| x |
| 2+3+4+5+6 |
| 5 |
. |
| y |
| 2+3+5+6+9 |
| 5 |
 |
| y |
| 2×2+3×3+4×5+5×6+6×9-5×4×5 |
| 4+9+16+25+36-5×16 |
 |
| y |
 |
| e |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 资金投入x | 2 | 3 | 4 | 5 | 6 |
| 利润y | 2 | 3 | 5 | 6 | 9 |
 |
| y |
 |
| b |
 |
| a |
 |
| b |
| |||||||
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 资金入x | 2 | 3 | 4 | 5 | 6 |
| 利润 y | 2 | 3 | 5 | 6 | 9 |
| 5 |
 |
| i=1 |
 |
| y |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 资金投入x | 2 | 3 | 4 | 5 | 6 |
| 利润y | 2 | 3 | 5 | 6 | 9 |
 |
| y |
| |||||||
|
查看答案和解析>>
科目:高中数学 来源:2013届广东省罗定市高二下学期期中质量检测文科数学试卷(解析版) 题型:解答题
通过市场调查,得到某产品的资金投入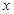 (万元)与获得的利润
(万元)与获得的利润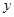 (万元)的数据,如下表所示:
(万元)的数据,如下表所示:
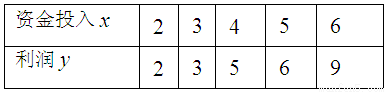
(1)画出数据对应的散点图;
(2)根据上表提供的数据,用最小二乘法求线性回归直线方程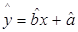 ;
;
(3)现投入资金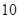 (万元),求估计获得的利润为多少万元.
(万元),求估计获得的利润为多少万元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com