
【题目】为增进市民的环保意识,某市有关部门面向全体市民进行了一次环保知识的微信问卷测试活动,每位市民仅有一次参与问卷测试机会.通过抽样,得到参与问卷测试的1000人的得分数据,制成频率分布直方图如图所示.

(1)估计成绩得分落在[86,100]中的概率.
(2)设这1000人得分的样本平均值为![]() .
.
(i)求![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(ii)有关部门为参与此次活动的市民赠送20元或10元的随机话费,每次获赠20元或10元的随机话费的概率分别为![]() 和
和![]() .得分不低于
.得分不低于![]() 的可获赠2次随机话费,得分低于
的可获赠2次随机话费,得分低于![]() 的可获赠1次随机话费.求一位市民参与这次活动获赠话费
的可获赠1次随机话费.求一位市民参与这次活动获赠话费![]() 的平均估计值.
的平均估计值.
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】(1)某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系![]() 自然对数的底数,k,b为常数),若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,求该食品在33℃的保鲜时间.
自然对数的底数,k,b为常数),若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,求该食品在33℃的保鲜时间.
(2)某药厂生产一种口服液,按药品标准要求其杂质含量不能超过0.01%,若初始时含杂质0.2%,每次过滤可使杂质含量减少三分之一,问至少应过滤几次才能使得这种液体达到要求?(已知![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有![]() 、
、![]() 、
、![]() 、
、![]() 四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖,在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下.
四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖,在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下.
甲说:“![]() 、
、![]() 同时获奖.”
同时获奖.”
乙说:“![]() 、
、![]() 不可能同时获奖.”
不可能同时获奖.”
丙说:“![]() 获奖.”
获奖.”
丁说:“![]() 、
、![]() 至少一件获奖”
至少一件获奖”
如果以上四位同学中有且只有两位同学的预测是正确的,则获奖的作品是( )
A. 作品![]() 与作品
与作品![]() B. 作品
B. 作品![]() 与作品
与作品![]() C. 作品
C. 作品![]() 与作品
与作品![]() D. 作品
D. 作品![]() 与作品
与作品![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(ax2+x+6).
(1)若a=﹣1,求f(x)的定义域,并讨论f(x)的单调性;
(2)若函数f(x)的定义域为R,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
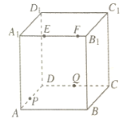
【题目】如图,正方体![]() 的棱长为4,动点E,F在棱
的棱长为4,动点E,F在棱![]() 上,动点P,Q分别在棱AD,CD上。若
上,动点P,Q分别在棱AD,CD上。若![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() 大于零),则四面体PEFQ的体积
大于零),则四面体PEFQ的体积
A.与![]() 都有关B.与m有关,与
都有关B.与m有关,与![]() 无关
无关
C.与p有关,与![]() 无关D.与π有关,与
无关D.与π有关,与![]() 无关
无关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,g(x)=f(x)﹣3.
,g(x)=f(x)﹣3.
(1)判断并证明函数g(x)的奇偶性;
(2)判断并证明函数g(x)在(1,+∞)上的单调性;
(3)若f(m2﹣2m+7)≥f(2m2﹣4m+4)成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com