Question

【题目】在中，给出如下命题:

①是所在平面内一定点，且满足，则是的垂心；

②是所在平面内一定点，动点满足，，则动点一定过的重心；

③是内一定点，且，则；

④若且，则为等边三角形，

其中正确的命题为_____（将所有正确命题的序号都填上）

Answer 1

【答案】①②④．

【解析】

①:运用已知的式子进行合理的变形，可以得到，进而得到，再次运用等式同样可以得到,，这样可以证明出是的垂心；

②：运用平面向量的减法的运算法则、加法的几何意义，结合平面向量共线定理，可以证明本命题是真命题；

③：运用平面向量的加法的几何意义以及平面向量共线定理，结合面积公式，可证明出本结论是错误的；

④：运用平面向量的加法几何意义和平面向量的数量积的定义，可以证明出本结论是正确的.

①: ，同理可得：,，所以本命题是真命题；

②: ，设的中点为，所以有，因此动点一定过的重心，故本命题是真命题；

③: 由，可得设的中点为，,

,故本命题是假命题；

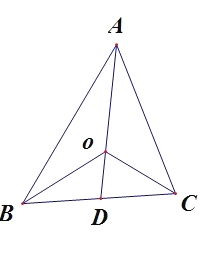
④: 由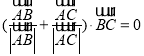可知角的平分线垂直于底边，故是等腰三角形，

由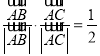可知：，所以是等边三角形，故本命题是真命题，因此正确的命题为①②④.