
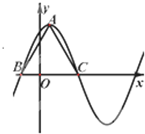
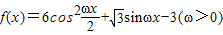 ,在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.
,在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.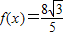 ,且
,且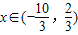 ,求f(x+1)的值.
,求f(x+1)的值.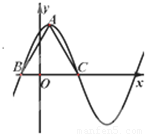
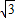 sin(ωx+
sin(ωx+ ),由正三角形△ABC的高为2
),由正三角形△ABC的高为2 可求得BC,从而可求得其周期,继而可得ω
可求得BC,从而可求得其周期,继而可得ω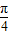 x+
x+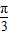 ∈[
∈[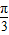 ,
,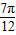 ],利用正弦函数的性质可求得函数f(x)的值域;
],利用正弦函数的性质可求得函数f(x)的值域;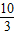 ,
, )可求得(
)可求得(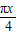 +
+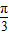 )∈(-
)∈(-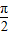 ,
, ),从而可求得cos(
),从而可求得cos( +
+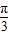 ),最后利用两角和的正弦即可求得f(x+1)的值.
),最后利用两角和的正弦即可求得f(x+1)的值. +
+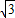 sinωx-3(ω>0)
sinωx-3(ω>0)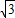 sinωx
sinωx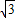 sin(ωx+
sin(ωx+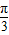 ),…3分
),…3分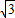 ,则BC=4,
,则BC=4,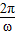 =8,
=8,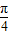 …5分
…5分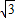 ,2
,2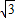 ]…6分
]…6分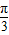 ≤
≤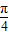 x+
x+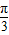 ≤
≤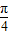 +
+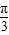 ,
,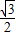 ≤sin(
≤sin(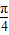 x+
x+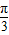 )≤
)≤ ,
,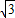 sin(
sin( +
+ )≤
)≤
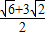 ]…(9分)
]…(9分)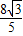 由(Ⅰ)有f(x)=2
由(Ⅰ)有f(x)=2 sin(
sin(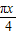 +
+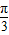 )=
)=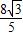 ,即sin(
,即sin(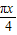 +
+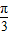 )=
)= ,
,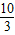 ,
, )得:(
)得:(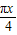 +
+ )∈(-
)∈(-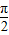 ,
, ),
),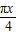 +
+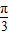 )=
)= =
= …(11分)
…(11分)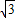 sin(
sin(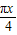 +
+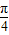 +
+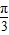 )=2
)=2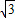 sin[(
sin[(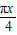 +
+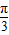 )+
)+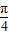 ]=2
]=2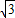 sin[(
sin[(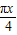 +
+ )cos
)cos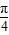 +cos(
+cos(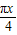 +
+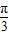 )sin
)sin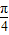
 (
( ×
×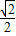 +
+ ×
× )=
)=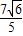 …13分
…13分

科目:高中数学 来源: 题型:
| a |
| π |
| 4 |
| b |
| 2 |
| a |
| b |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 6 |
| π |
| 12 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知函数f(x)=6cos2
已知函数f(x)=6cos2| ωx |
| 2 |
| 3 |
8
| ||
| 5 |
| 10 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:山东省曲阜师范大学附中2006~2007学年度第二学期期末考试、高一数学试题 题型:044
已知函数![]() ,在一个周期内的图象如图所示.
,在一个周期内的图象如图所示.
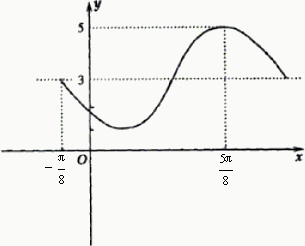
(I)求此函数的解析式;
(II)求当x∈R时函数y的最大值、最小值及函数取得最大值、最小值时的自变量x的值;
(III)讨论函数在[0,π]内的单调性;
(IV)求出不等式y>4的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com