
分析 (1)根据已知条件有$\left\{\begin{array}{l}{f(-2)=4a-2b+c=0}\\{f(0)=c=0}\\{\frac{4ac-{b}^{2}}{4a}=-1}\end{array}\right.$,这样便可解出a=1,b=2,c=0,从而f(x)=x2+2x;
(2)求g(x)=(1-m)x2-2(1+m)x+1,根据g(x)是否为二次函数,讨论m:m=1时,容易判断出符合条件,m<1,m>1时,g(x)都为二次函数,根据二次函数的单调区间和对称轴的关系即可求出m的范围,并上m=1即可得出m的范围;
(3)求出h(x)=$lo{g}_{2}(-{x}^{2}-2x+n)$,该函数无零点,从而有-x2-2x+n>0,且-x2-2x+n≠1,由判别式的取值即可得出n的范围.
解答 解:(1)由条件$\left\{\begin{array}{l}{4a-2b+c=0}\\{c=0}\\{\frac{4ac-{b}^{2}}{4a}=-1}\end{array}\right.$;
解得a=1,b=2,c=0;
∴f(x)=x2+2x;
(2)g(x)=(1-m)x2-2(1+m)x+1;
①若m=1,则g(x)=-4x+1满足在[-1,1]上为减函数;
②若m<1,1-m>0,g(x)的对称轴为x=$\frac{1+m}{1-m}$;
g(x)在[-1,1]上为减函数;
∴$\frac{1+m}{1-m}≥1$;
解得0≤m<1;
③若m>1,1-m<0;
∴$\frac{1+m}{1-m}≤-1$;
解得m>1;
∴综上得实数m的范围为[0,+∞);
(3)h(x)=$lo{g}_{2}(-{x}^{2}-2x+n)$则-x2-2x+n>0,且-x2-2x+n≠1;
-x2-2x+n>0;
∴△=4+4n>0;
∴n>-1;
-x2-2x+n≠1;
∴-x2-2x+n-1≠0;
∴△=4+4(n-1)<0;
∴n<0;
∴-1<n<0;
∴n的范围为(-1,0).
点评 考查求二次函数最值的公式,已知函数解析式求值,二次函数单调性和其对称轴的关系,以及解分式不等式,函数零点的定义,一元二次方程是否有解与判别式取值的关系,要熟悉二次函数的图象.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 资金投入x | 2 | 3 | 4 | 5 | 6 |
| 利润y | 2 | 3 | 5 | 6 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
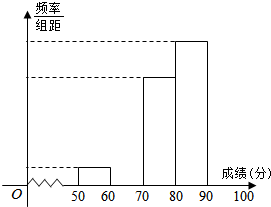 青少年“心理健康”问题越来越引起社会关注,某校对高一600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正整数,满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
青少年“心理健康”问题越来越引起社会关注,某校对高一600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正整数,满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.| 分组 | 频数 | 频率 |
| [50,60) | 2 | 0.04 |
| [60,70) | 8 | 0.16 |
| [70,80) | 10 | |
| [80,90) | ||
| [90,100] | 14 | 0.28 |
| 合计 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com