
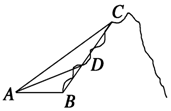
 如图,嵩山上原有一条笔直的山路BC,现在又新架设了 一条索道AC,李在山脚B处看索道AC,发现张角∠ABC=120°;从B处攀登4千米到达D处,回头看索道AC,发现张角∠ADC=150°;从D处再攀登8千米方到达C处,索道AC的长为$4\sqrt{13}$千米.
如图,嵩山上原有一条笔直的山路BC,现在又新架设了 一条索道AC,李在山脚B处看索道AC,发现张角∠ABC=120°;从B处攀登4千米到达D处,回头看索道AC,发现张角∠ADC=150°;从D处再攀登8千米方到达C处,索道AC的长为$4\sqrt{13}$千米. 分析 在△ABC中根据∠ABD=120°,∠ADB=180°-∠ADC=30°,利用内角和定理算出∠DAB=30°,从而AB=BD=4千米,利用余弦定理算出AD=4$\sqrt{3}$.然后在△ADC中,根据两边AD、DC长和夹角∠ADC=150°,利用余弦定理解出AC2值,从而得出AC.
解答 解:在△ABD中,BD=4千米,∠ABD=120°,
∵∠ADB=180°-∠ADC=30°
∴∠DAB=180°-120°-30°=30°
得△ABD中,AB=BD=4千米,AD=4$\sqrt{3}$(千米)
在△ADC中,DC=8千米,∠ADC=150°
∴AC2=AD2+DC2-2 AD•DC•cos∠ADC
=42×3+82-2×4$\sqrt{3}$×8×cos150°=208(千米)
∴AC=$4\sqrt{13}$千米.
故答案为$4\sqrt{13}$.
点评 本题以山上的索道为例,求嵩山的一条索道AC之长.着重考查了三角形内角和定理、利用正余弦定理解三角形等知识,属于中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 31 | C. | 16 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com