
分析 (1)判断题目是关于等差数列的知识,然后列出f(n)的关系式,令f(n)>15求出n,可得车主第5年开始获利超过25万元;
(2)对方案一:利润f(n)=-(n-10)2+51求出最大值,对方案二:年平均获利,得到n=7时,年平均获利最大,然后建议车主采用方案二处理这条货车.
解答 (本题满分12分)
解:(1)每年的费用支出是以6为首项,2为公差的等差数列,…(1分)
依题意$f(n)=25n-[6n+\frac{n(n-1)}{2}×2]-49=-{n^2}+20n-49$…(3分)
令f(n)>15得n2-20n+64<0,解得4<n<16…(5分)
故车主第5年开始获利超过25万元; …(6分)
(2)对方案一:利润f(n)=-(n-10)2+51
所以当n=10时,利润取得最大值,为51万元
此时出售货车,共获利51+4=55万元 …(8分)
对方案二:年平均获利$\frac{f(n)}{n}=20-(n+\frac{49}{n})≤20-2\sqrt{49}=6$万元
所以当$n=\frac{49}{n}$即n=7时,年平均获利最大,…(10分)
此时出售货车,共获利6×7+13=55万元 …(11分)
这两种方案车主均获利55万元,但方案一用时10年,而方案二只需7年,用时较少,故建议车主采用方案二处理这条货车 …(12分)
点评 本题考查数列在函数中的应用,考查分析问题解决问题的能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
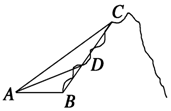 如图,嵩山上原有一条笔直的山路BC,现在又新架设了 一条索道AC,李在山脚B处看索道AC,发现张角∠ABC=120°;从B处攀登4千米到达D处,回头看索道AC,发现张角∠ADC=150°;从D处再攀登8千米方到达C处,索道AC的长为$4\sqrt{13}$千米.
如图,嵩山上原有一条笔直的山路BC,现在又新架设了 一条索道AC,李在山脚B处看索道AC,发现张角∠ABC=120°;从B处攀登4千米到达D处,回头看索道AC,发现张角∠ADC=150°;从D处再攀登8千米方到达C处,索道AC的长为$4\sqrt{13}$千米.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com