练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．已知两个等差数列{an}和{bn}的前n项和分别是Sn和Tn，且对任意正整数n都有$\frac{{S}_{n}}{{T}_{n}}$=$\frac{3n+5}{2n+3}$，则$\frac{{a}_{7}}{{b}_{7}}$=$\frac{44}{29}$．

    分析 利用等差数列的通项公式与求和公式及其性质即可得出．

    解答 解：$\frac{{a}_{7}}{{b}_{7}}$=$\frac{\frac{13（{a}_{1}+{a}_{13}）}{2}}{\frac{13（{b}_{1}+{b}_{13}）}{2}}$=$\frac{{S}_{13}}{{T}_{13}}$=$\frac{3×13+5}{2×13+3}$=$\frac{44}{29}$．
    故答案为：$\frac{44}{29}$．

    点评 本题考查了等差数列的通项公式及其性质，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

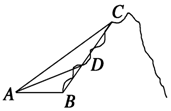    9．如图，嵩山上原有一条笔直的山路BC，现在又新架设了 一条索道AC，李在山脚B处看索道AC，发现张角∠ABC=120°；从B处攀登4千米到达D处，回头看索道AC，发现张角∠ADC=150°；从D处再攀登8千米方到达C处，索道AC的长为$4\sqrt{13}$千米．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知变量x，y满足约束条件$\left\{\begin{array}{l}{y≤2}\\{x+y≥4}\\{x-y≤1}\end{array}\right.$，则z=3x+y的最大值为（　　）
    A．8B．11C．9D．12

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．若目标函数z=ax+by（a＞0，b＞0）满足约束条件$\left\{\begin{array}{l}{2x-y-6≤0}\\{x-y+2≥0}\\{x≥0，y≥0}\end{array}\right.$且最大值为40，则$\frac{5}{a}$+$\frac{1}{b}$的最小值为（　　）
    A．1B．$\frac{9}{4}$C．4D．$\frac{25}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．下列函数为同一函数的是（　　）
    A．y=x2-2x和y=t2-2tB．y=x0和y=1
    C．y=$\sqrt{（x+1）^{2}}$和y=x+1D．y=lgx2和y=2lgx

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．若点M是△ABC所在平面内的一点，且满足5$\overrightarrow{AM}$=$\overrightarrow{AB}$+3$\overrightarrow{AC}$，则△MBC与△ABC的面积比为（　　）
    A．$\frac{1}{5}$B．$\frac{2}{5}$C．$\frac{3}{5}$D．$\frac{4}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知集合A=[1，4]，B=（-∞，a），若A⊆∁BB，则实数a的取值范围为（-∞，1]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．在△ABC中，角A、B、C的对边分别为a、b、c，若acosB+bcosA=csinA，则△ABC的形状为（　　）
    A．直角三角形B．钝角三角形C．锐角三角形D．不确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．函数f（x）=x2-2ax+2在（-∞，6）内递减，则a的取值范围为[6，+∞）．

    查看答案和解析>>

    同步练习册答案