
分析 由数列的通项公式可得$\underset{lim}{n→∞}$an=$\underset{lim}{n→∞}$$\frac{2n+1}{5n+1}$,再由$\underset{lim}{n→∞}$$\frac{1}{n}$=0,即可得到所求值.
解答 解:由数列{an}的通项公式an=$\left\{\begin{array}{l}{(\frac{1}{3})^{n},1≤n≤100}\\{\frac{2n+1}{5n-1},n>100}\end{array}\right.$,
可得$\underset{lim}{n→∞}$an=$\underset{lim}{n→∞}$$\frac{2n+1}{5n+1}$=$\underset{lim}{n→∞}$$\frac{2+\frac{1}{n}}{5+\frac{1}{n}}$=$\frac{2+0}{5+0}$=$\frac{2}{5}$.
故答案为:$\frac{2}{5}$.
点评 本题考查数列极限的运算,注意运用$\underset{lim}{n→∞}$$\frac{1}{n}$=0,考查运算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 等腰三角形 | D. | 等腰或直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
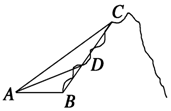 如图,嵩山上原有一条笔直的山路BC,现在又新架设了 一条索道AC,李在山脚B处看索道AC,发现张角∠ABC=120°;从B处攀登4千米到达D处,回头看索道AC,发现张角∠ADC=150°;从D处再攀登8千米方到达C处,索道AC的长为$4\sqrt{13}$千米.
如图,嵩山上原有一条笔直的山路BC,现在又新架设了 一条索道AC,李在山脚B处看索道AC,发现张角∠ABC=120°;从B处攀登4千米到达D处,回头看索道AC,发现张角∠ADC=150°;从D处再攀登8千米方到达C处,索道AC的长为$4\sqrt{13}$千米.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(λ)先增大后减小,且最小值为1 | B. | f(λ)先减小后增大,且最小值为1 | ||
| C. | f(λ)先减小后增大,且最小值为$\frac{{\sqrt{5}}}{5}$ | D. | f(λ)先增大后减小,且最小值为$\frac{{\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 11 | C. | 9 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com