
分析 (1)由|x+6|+|x-1|≥|x+6-x+1|=7,能求出m 的取值范围.
(2)当m取最大值时,m=7,原不等式等价于:|x-4|-3x≤5,由此能求出原不等式的解集.
解答 解:(1)∵|x+6|+|x-1|≥|x+6-x+1|=7,
又对于任意实数x,不等式|x+6|+|x-1|≥m恒成立,
∴m≤7,
∴m 的取值范围是(-∞,7].
(2)当m取最大值时,m=7,
原不等式等价于:|x-4|-3x≤5,
∴$\left\{\begin{array}{l}{x≥4}\\{x-4-3x≤5}\end{array}\right.$或$\left\{\begin{array}{l}{x<4}\\{4-x-3x≤5}\end{array}\right.$,
解得x≥4或-$\frac{1}{4}$≤x<4,
∴原不等式的解集为{x|x≥-$\frac{1}{4}$}.
点评 本题考查实数的取值范围的求法,考查绝对值不等式的解法,是中档题,解题时要认真审题,注意含绝对值不等式的性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (1,2) | C. | (1,2] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
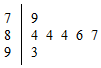 某校举行元旦汇演,七位评委为某班的小品打出的分数如茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差是$\frac{8}{5}$.
某校举行元旦汇演,七位评委为某班的小品打出的分数如茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差是$\frac{8}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com