【答案】
分析:(Ⅰ)求出函数f(x)=x-4
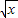
+4(x≥4)的反函数,把a
n+1=f
-1(a
n)代入,整理后即可证明数列{
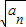
}为等差数列;
(Ⅱ)由数列{
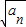
}为等差数列求出数列{
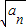
}通项公式,进一步得到数列{a
n}的通项公式,再由数列b
1,b
2-b
1,b
3-b
2,…,b
n-b
n-1是首项为1,公比为

的等比数列,求出{b
n}的通项公式,代入c
n=
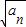
•b
n后化简,然后利用分组求和和错位相减法求和可得数列{c
n}的前n项和S
n.
解答:(Ⅰ)证明:∵函数f(x)=x-4
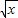
+4(x≥4),即
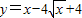
(x≥4),
∴
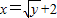
(y≥0),∴
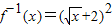
(x≥2),
∴a
n+1=f
-1(a
n)=
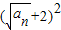
,
即
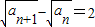
(n∈N
*).
∴数列{
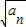
}是以
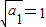
为首项,公差为2的等差数列.
(Ⅱ)解:由(Ⅰ)得:
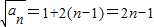
,
即
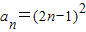
(n∈N
*).
由b
1=1,当n≥2时,
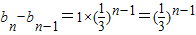
,
∴b
n=b
1+(b
2-b
1)+(b
3-b
2)+…+(b
n-b
n-1)
=
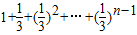
=
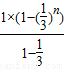
=
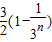
.
因而
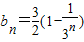
(n∈N
*).
由c
n=
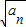
•b
n,得:
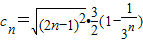
=
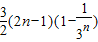
,
∴S
n=c
1+c
2+…+c
n=
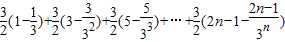
=
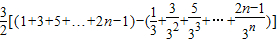
.
令
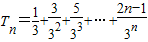
①
则
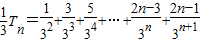
②
①-②得,
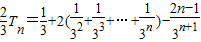
=
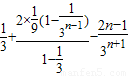
=
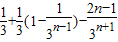
.
∴
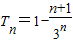
.
又1+3+5+…+(2n-1)=n
2.
∴
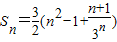
.
点评:本题考查了由递推式确定数列是等差数列,考查了等比数列的性质,训练了等差数列和等比数列通项公式的求法,考查了利用分组法和错位相减法求数列的前n项和,求一个等差数列和一个等比数列的积数列的前n项和,一般都用错位相减法,此题是中档题.

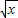 +4(x≥4)的反函数为f-1(x),数列{an}满足:a1=1,an+1=f-1(an),(n∈N*),数列b1,b2-b1,b3-b2,…,bn-bn-1是首项为1,公比为
+4(x≥4)的反函数为f-1(x),数列{an}满足:a1=1,an+1=f-1(an),(n∈N*),数列b1,b2-b1,b3-b2,…,bn-bn-1是首项为1,公比为 的等比数列.
的等比数列.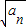 }为等差数列;
}为等差数列;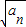 •bn,求数列{cn}的前n项和Sn.
•bn,求数列{cn}的前n项和Sn.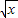 +4(x≥4)的反函数,把an+1=f-1(an)代入,整理后即可证明数列{
+4(x≥4)的反函数,把an+1=f-1(an)代入,整理后即可证明数列{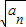 }为等差数列;
}为等差数列;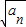 }为等差数列求出数列{
}为等差数列求出数列{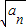 }通项公式,进一步得到数列{an}的通项公式,再由数列b1,b2-b1,b3-b2,…,bn-bn-1是首项为1,公比为
}通项公式,进一步得到数列{an}的通项公式,再由数列b1,b2-b1,b3-b2,…,bn-bn-1是首项为1,公比为 的等比数列,求出{bn}的通项公式,代入cn=
的等比数列,求出{bn}的通项公式,代入cn=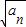 •bn后化简,然后利用分组求和和错位相减法求和可得数列{cn}的前n项和Sn.
•bn后化简,然后利用分组求和和错位相减法求和可得数列{cn}的前n项和Sn.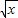 +4(x≥4),即
+4(x≥4),即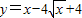 (x≥4),
(x≥4),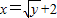 (y≥0),∴
(y≥0),∴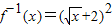 (x≥2),
(x≥2),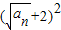 ,
,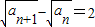 (n∈N*).
(n∈N*).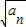 }是以
}是以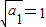 为首项,公差为2的等差数列.
为首项,公差为2的等差数列.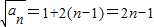 ,
,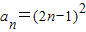 (n∈N*).
(n∈N*).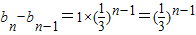 ,
,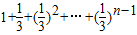
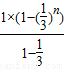
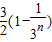 .
.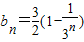 (n∈N*).
(n∈N*).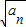 •bn,得:
•bn,得: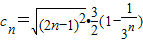 =
=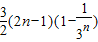 ,
,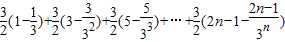
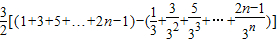 .
.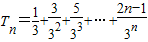 ①
①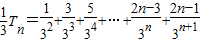 ②
②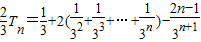
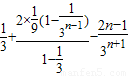
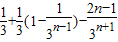 .
.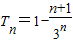 .
.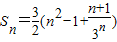 .
.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<