
分析 (1)求出f(x)的导数,可得切线的斜率和切点,由已知切线的方程,即可得到a,b的值;
(2)求出PQ的中点坐标,分别求出f(x),g(x)的导数,可得斜率k1,k2,化简整理,法一:令r(t)=lnt-$\frac{2(t-1)}{1+t}$,t=$\frac{{x}_{2}}{{x}_{1}}$>1,求出r(t)的导数,判断单调性,即可得证;法二:令m(t)=(t+1)lnt-2(t-1),t=$\frac{{x}_{2}}{{x}_{1}}$>1,求出m(t)的导数,判断单调性,可得证明.
解答 解:(1)直线x-y-1=0的斜率为1,且过(1,0)点,
又函数f(x)=logax+b的导数为f′(x)=$\frac{1}{xlna}$,
检验$\frac{1}{lna}$=1,loga1+b=0,
解得a=e,b=0;
(2)证明:PQ的中点为($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$),f(x)=lnx,f′(x)=$\frac{1}{x}$,
可得k1=$\frac{1}{\frac{{x}_{1}+{x}_{2}}{2}}$=$\frac{2}{{x}_{1}+{x}_{2}}$,
g(x)=mx+$\frac{n}{x}$的导数为g′(x)=m-$\frac{n}{{x}^{2}}$,
即有k2=m-$\frac{n}{(\frac{{x}_{1}+{x}_{2}}{2})^{2}}$,
由x1>x2>0,可得($\frac{{x}_{1}+{x}_{2}}{2}$)2>x1x2,
即有k2>m-$\frac{n}{{x}_{1}{x}_{2}}$,
则(x2-x1)k2>m(x2-x1)-$\frac{n({x}_{2}-{x}_{1})}{{x}_{1}{x}_{2}}$
=mx2+$\frac{n}{{x}_{2}}$-(mx1+$\frac{n}{{x}_{1}}$)=y2-y1=lnx2-lnx1=ln$\frac{{x}_{2}}{{x}_{1}}$,
又(x2-x1)k1=$\frac{2({x}_{2}-{x}_{1})}{{x}_{1}+{x}_{2}}$=$\frac{2(\frac{{x}_{2}}{{x}_{1}}-1)}{1+\frac{{x}_{2}}{{x}_{1}}}$,
法一:令r(t)=lnt-$\frac{2(t-1)}{1+t}$,t=$\frac{{x}_{2}}{{x}_{1}}$>1,则r′(t)=$\frac{1}{t}$-$\frac{4}{(t+1)^{2}}$=$\frac{(t-1)^{2}}{t(t+1)^{2}}$,
因为t>1时,r′(t)>0,所以r(t)在[1,+∞)上单调递增,
故r(t)>r(1)=0,则k2>k1.
法二:令m(t)=(t+1)lnt-2(t-1),t=$\frac{{x}_{2}}{{x}_{1}}$>1,则m′(t)=lnt+$\frac{1}{t}$-1,
因为(lnt+$\frac{1}{t}$)′=$\frac{1}{t}$-$\frac{1}{{t}^{2}}$=$\frac{t-1}{{t}^{2}}$,所以t>1时,(lnt+$\frac{1}{t}$)′>0,
故lnt+$\frac{1}{t}$在[1,+∞)上单调递增,从而lnt+$\frac{1}{t}$-1>0,即r′(t),
于是m(t)在[1,+∞)上单调递增,故m(t)>m(1)=0,
即(t+1)lnt>2(t-1),即lnt>$\frac{2(t-1)}{1+t}$,
则k2>k1.
点评 本题考查导数的运用:求切线的斜率和求单调区间,考查不等式的证明,注意运用导数的几何意义和斜率公式,以及构造函数求出导数,判断单调性,考查化简整理的运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=3sin2x | B. | y=3sin$\frac{1}{2}$x | C. | $y=\frac{1}{3}sin2x$ | D. | $y=\frac{1}{3}sin\frac{1}{2}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在物理实验中,为了研究所挂物体的重量x对弹簧长度y的影响.某学生通过实验测量得到物体的重量与弹簧长度的对比表:
在物理实验中,为了研究所挂物体的重量x对弹簧长度y的影响.某学生通过实验测量得到物体的重量与弹簧长度的对比表:| 物体重量(单位g) | 1 | 2 | 3 | 4 | 5 |
| 弹簧长度(单位cm) | 1.5 | 3 | 4 | 5 | 6.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
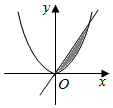 双曲线:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率为m,记函数y=x2与y=mx的图象所围成的阴影部分的面积为S(如图所示),任取x∈[0,2],y∈[0,4],则点(x,y)恰好落在阴影区域内的概率为( )
双曲线:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率为m,记函数y=x2与y=mx的图象所围成的阴影部分的面积为S(如图所示),任取x∈[0,2],y∈[0,4],则点(x,y)恰好落在阴影区域内的概率为( )| A. | $\frac{17}{96}$ | B. | $\frac{5}{32}$ | C. | $\frac{1}{6}$ | D. | $\frac{7}{48}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 1+$\sqrt{2}$ | D. | 1+$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com