
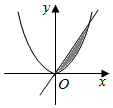
 双曲线:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率为m,记函数y=x2与y=mx的图象所围成的阴影部分的面积为S(如图所示),任取x∈[0,2],y∈[0,4],则点(x,y)恰好落在阴影区域内的概率为( )
双曲线:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率为m,记函数y=x2与y=mx的图象所围成的阴影部分的面积为S(如图所示),任取x∈[0,2],y∈[0,4],则点(x,y)恰好落在阴影区域内的概率为( )| A. | $\frac{17}{96}$ | B. | $\frac{5}{32}$ | C. | $\frac{1}{6}$ | D. | $\frac{7}{48}$ |
分析 根据双曲线的性质求出离心率m,求出交点坐标,结合积分的应用求出阴影部分的面积,利用几何概型的概率公式进行计算即可.
解答 解:由$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1得a2=4,b2=12,
则c2=4+12=16,
即a=2,c=4,则离心率为m=$\frac{c}{a}$=$\frac{4}{2}$=2,
则直线y=mx=2x代入y=x2,得x2=2x,
则x=0或x=2,
则阴影部分的面积S=∫${\;}_{0}^{2}$(2x-x2)dx=(x2-$\frac{1}{3}$x3)|${\;}_{0}^{2}$=4-$\frac{8}{3}$=$\frac{4}{3}$,
∵x∈[0,2],y∈[0,4],
∴对应矩形的面积S=2×4=8,
则则点(x,y)恰好落在阴影区域内的概率P=$\frac{\frac{4}{3}}{8}$=$\frac{1}{6}$,
故选:C
点评 本题主要考查几何概型的概率的计算,根据双曲线的性质求出离心率以及利用积分求出阴影部分的面积是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}-\frac{3}{4π}$ | B. | $\frac{1}{3}+\frac{{\sqrt{3}}}{4π}$ | C. | $\frac{1}{2}-\frac{{\sqrt{3}}}{4π}$ | D. | $\frac{1}{3}-\frac{{\sqrt{3}}}{4π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0)∪(0,+∞) | B. | (-∞,0)∪(0,1) | C. | (-1,0)∪(0,1) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com