
分析 (1)优先考虑特殊元素“老师”,老师在中间5个位置选一个有5种排法,其余的6名同学在剩下的6个位置经行全排列即可;
(2)正难则反的原则,先求出没有限制的排列,再排除“只选男生或只选女生”的种数,问题得以解决.
(3)转化法,此题相当于“安排5个节目,其中3个节目相对顺序确定,有多少种方法?”问题得以解决.
解答 解:(1)优先考虑特殊元素“老师”,老师在中间5个位置选一个有5种排法,其余的6名同学在剩下的6个位置经行全排列有A66=720种排法,
故有5×720=3600种.
(2)从反面考虑,“男女至少各1名”的反面是“只选男生或只选女生”.
只选男生有C64=15种情况,只选女生有C54=5种情况,所以反面共有15+5=20种,
从6名男生、5名女生中任选4人的所有情况共有C114=330种.故所求为330-20=310种不同选法.
(3)“添进去2个新节目”后,共有5个节目,因此,此题相当于“安排5个节目,其中3个节目相对顺序确定,有多少种方法?”
由于“3个节目相对顺序确定”,可以直接采用归一法.安排5种节目有A55=120种,三个节目对的全排列为A33=6种,
所以,一共有120÷6=20种安排方法.
点评 本题考查排列、组合及简单计数问题,关键是对题意的正确理解及分步计数原理的正确应用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | y=3sin2x | B. | y=3sin$\frac{1}{2}$x | C. | $y=\frac{1}{3}sin2x$ | D. | $y=\frac{1}{3}sin\frac{1}{2}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
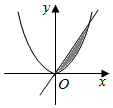 双曲线:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率为m,记函数y=x2与y=mx的图象所围成的阴影部分的面积为S(如图所示),任取x∈[0,2],y∈[0,4],则点(x,y)恰好落在阴影区域内的概率为( )
双曲线:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率为m,记函数y=x2与y=mx的图象所围成的阴影部分的面积为S(如图所示),任取x∈[0,2],y∈[0,4],则点(x,y)恰好落在阴影区域内的概率为( )| A. | $\frac{17}{96}$ | B. | $\frac{5}{32}$ | C. | $\frac{1}{6}$ | D. | $\frac{7}{48}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{27}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{7}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 1+$\sqrt{2}$ | D. | 1+$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com