
| A. | $\frac{8}{27}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{7}{27}$ |
分析 求出函数与x轴和y=$\frac{1}{3}$x的交点坐标,根据积分的几何意义求出对应的区域面积,结合几何概型的概率公式进行计算即可.
解答 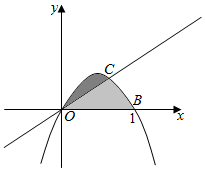 解:由f(x)=x-x2=0得x=0或x=1,即B(1,0)
解:由f(x)=x-x2=0得x=0或x=1,即B(1,0)
由$\left\{\begin{array}{l}{y=x-{x}^{2}}\\{y=\frac{1}{3}x}\end{array}\right.$得x-x2=$\frac{1}{3}$x,得$\frac{2}{3}$x=x2,
得x=0或x=$\frac{2}{3}$,即C($\frac{2}{3}$,0),
由积分的定义得区域A的面积S=∫${\;}_{0}^{1}$(x-x2)dx=($\frac{1}{2}$x2-$\frac{1}{3}$x3)|${\;}_{0}^{1}$=$\frac{1}{2}$-$\frac{1}{3}$=$\frac{1}{6}$,
区域M的面积S=∫${\;}_{0}^{\frac{2}{3}}$(x-x2-$\frac{1}{3}$x)dx=($\frac{1}{3}$x2-$\frac{1}{3}$x3)|${\;}_{0}^{\frac{2}{3}}$=[$\frac{1}{3}$($\frac{2}{3}$)2-$\frac{1}{3}$($\frac{2}{3}$)3]|=$\frac{4}{27}$-$\frac{8}{81}$=$\frac{4}{81}$,
则若向区域M内随机抛掷一点P,则点P落在区域A的概率P=$\frac{\frac{4}{81}}{\frac{1}{6}}$=$\frac{8}{27}$,
故选:A.
点评 本题主要考查几何概型的概率的计算,根据积分求出对应区域的面积是解决本题的关键.考查学生的转化和计算能力.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0)∪(0,+∞) | B. | (-∞,0)∪(0,1) | C. | (-1,0)∪(0,1) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
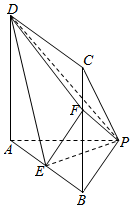 在四棱锥P-ABCD中,底面ABCD是矩形,DA⊥平面ABP,E是棱AB的中点,F在棱BC上,且AP=BP=$\sqrt{2}$,AB=2,AD=3,BF=2.
在四棱锥P-ABCD中,底面ABCD是矩形,DA⊥平面ABP,E是棱AB的中点,F在棱BC上,且AP=BP=$\sqrt{2}$,AB=2,AD=3,BF=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 54种 | B. | 48种 | C. | 42种 | D. | 36种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄x | 6 | 7 | 8 | 9 |
| 身高y | 118 | 126 | 136 | 144 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com