
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
分析 根据双曲线的定义结合余弦定理进行转化求解即可.
解答 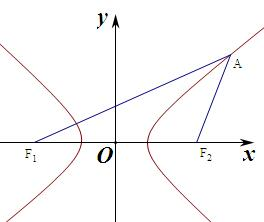 解:∵|AF1|=2|AF2|,
解:∵|AF1|=2|AF2|,
∴点A在双曲线的右支上,
∵|AF1|-|AF2|=2|AF2|-|AF2|=|AF2|=2a,
∴|AF1|=4a,
∵双曲线的离心率为$\sqrt{3}$,
∴e=$\sqrt{3}$,
则cos∠F1AF2=$\frac{A{{F}_{1}}^{2}+A{{F}_{2}}^{2}-{F}_{1}{F}_{2}}{2A{F}_{1}A{F}_{2}}$=$\frac{16{a}^{2}+4{a}^{2}-4{c}^{2}}{2×2a•4a}$=$\frac{20{a}^{2}-4{c}^{2}}{16{a}^{2}}$=$\frac{20}{16}$-$\frac{1}{4}$•$\frac{{c}^{2}}{{a}^{2}}$=$\frac{5}{4}$-$\frac{1}{4}$•e2=$\frac{5}{4}$-$\frac{1}{4}$×3=$\frac{2}{4}=\frac{1}{2}$,
故选:D
点评 本题主要考查双曲线的性质以及余弦定理的应用,根据条件结合双曲线的定义建立方程关系是解决本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=3sin2x | B. | y=3sin$\frac{1}{2}$x | C. | $y=\frac{1}{3}sin2x$ | D. | $y=\frac{1}{3}sin\frac{1}{2}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在物理实验中,为了研究所挂物体的重量x对弹簧长度y的影响.某学生通过实验测量得到物体的重量与弹簧长度的对比表:
在物理实验中,为了研究所挂物体的重量x对弹簧长度y的影响.某学生通过实验测量得到物体的重量与弹簧长度的对比表:| 物体重量(单位g) | 1 | 2 | 3 | 4 | 5 |
| 弹簧长度(单位cm) | 1.5 | 3 | 4 | 5 | 6.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
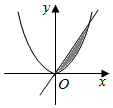 双曲线:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率为m,记函数y=x2与y=mx的图象所围成的阴影部分的面积为S(如图所示),任取x∈[0,2],y∈[0,4],则点(x,y)恰好落在阴影区域内的概率为( )
双曲线:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率为m,记函数y=x2与y=mx的图象所围成的阴影部分的面积为S(如图所示),任取x∈[0,2],y∈[0,4],则点(x,y)恰好落在阴影区域内的概率为( )| A. | $\frac{17}{96}$ | B. | $\frac{5}{32}$ | C. | $\frac{1}{6}$ | D. | $\frac{7}{48}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{27}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{7}{27}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com