
| A. | $\frac{1}{3}-\frac{3}{4π}$ | B. | $\frac{1}{3}+\frac{{\sqrt{3}}}{4π}$ | C. | $\frac{1}{2}-\frac{{\sqrt{3}}}{4π}$ | D. | $\frac{1}{3}-\frac{{\sqrt{3}}}{4π}$ |
分析 首先由题意画出图形,分别求出圆的面积以及满足y≤$\frac{{\sqrt{3}}}{3}$x的区域面积,利用几何概型的概率公式解答.
解答  解:由|z|≤2,得到(x-1)2+(y-$\sqrt{3}$)2≤4,对应的图形为以(1,$\sqrt{3}$)为圆心,2为半径的圆,面积为4π;满足如y≤$\frac{{\sqrt{3}}}{3}$x的是图中阴影部分,面积为$\frac{1}{3}•4π-\frac{1}{2}×2\sqrt{3}×1$,如图
解:由|z|≤2,得到(x-1)2+(y-$\sqrt{3}$)2≤4,对应的图形为以(1,$\sqrt{3}$)为圆心,2为半径的圆,面积为4π;满足如y≤$\frac{{\sqrt{3}}}{3}$x的是图中阴影部分,面积为$\frac{1}{3}•4π-\frac{1}{2}×2\sqrt{3}×1$,如图
所以所求概率为$\frac{{S}_{阴影}}{{S}_{圆}}$=$\frac{\frac{1}{3}•4π-\frac{1}{2}•2\sqrt{3}•1}{4π}$=$\frac{1}{3}-\frac{\sqrt{3}}{4π}$;
故选:D.
点评 本题考查了几何概型的概率求法;关键是正确画出图形,利用面积比求概率.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在物理实验中,为了研究所挂物体的重量x对弹簧长度y的影响.某学生通过实验测量得到物体的重量与弹簧长度的对比表:
在物理实验中,为了研究所挂物体的重量x对弹簧长度y的影响.某学生通过实验测量得到物体的重量与弹簧长度的对比表:| 物体重量(单位g) | 1 | 2 | 3 | 4 | 5 |
| 弹簧长度(单位cm) | 1.5 | 3 | 4 | 5 | 6.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
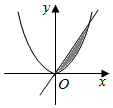 双曲线:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率为m,记函数y=x2与y=mx的图象所围成的阴影部分的面积为S(如图所示),任取x∈[0,2],y∈[0,4],则点(x,y)恰好落在阴影区域内的概率为( )
双曲线:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率为m,记函数y=x2与y=mx的图象所围成的阴影部分的面积为S(如图所示),任取x∈[0,2],y∈[0,4],则点(x,y)恰好落在阴影区域内的概率为( )| A. | $\frac{17}{96}$ | B. | $\frac{5}{32}$ | C. | $\frac{1}{6}$ | D. | $\frac{7}{48}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 运动时间 性别 | 运动达人 | 非运动达人 | 合计 |
| 男生 | 36 | ||
| 女生 | 26 | ||
| 合计 | 100 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com