练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    两圆相交于(1，3)和(m，－1)两点，两圆圆心都在直线x－y＋c＝0上，且m，c均为实数，则m＋c＝(　　)

    A．0  B．1

    C．2  D．3


    D　

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设α,β是两个不同的平面,l,m为两条不同的直线,命题p:若α∥β,l⊂α,m⊂β,则l∥m;命题q:若l∥α,m⊥l,m⊂β,则α⊥β.下列命题为真命题的是(　　)

    (A)p∨q      (B)p∧q  (C)(􀱑p)∨q   (D)p∧(􀱑q)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在空间直角坐标系Oxyz中,已知A(2,0,0),B(2,2,0),C(0,2,0),D(1,1,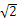).若S1,S2,S3分别为三棱锥DABC在xOy,yOz,zOx坐标平面上的正投影图形的面积,则(　)

    (A)S1=S2=S3         (B)S2=S1且S2≠S3

    (C)S3=S1且S3≠S2 (D)S3=S2且S3≠S1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图,在长方体ABCDA1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.

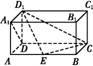
    (1)求异面直线D1E与A1D所成的角;

    (2)若二面角D1ECD的大小为45°,求点B到平面D1EC的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    圆x2＋y2－4x＝0在点P(1，)处的切线方程为______________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知椭圆W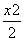：＋y2＝1，直线l与W相交于M，N两点，l与x轴、y轴分别相交于C，D两点，O为坐标原点．

    (1)若直线l的方程为x＋2y－1＝0，求△OCD外接圆的方程．

    (2)判断是否存在直线l，使得C，D是线段MN的两个三等分点．若存在，求出直线l的方程；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    观察下列数表的规律：

    图K37­2

    则从数2009到2010的箭头方向是(　　)

    A．→  B．↑

    C．←  D．↓

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知三棱锥S ­ ABC的三视图如图K38­1所示．在原三棱锥中给出下列结论：

    ①BC⊥平面SAC；②平面SBC⊥平面SAB；③SB⊥AC.

    其中，正确的结论是________(填序号)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图K40?7所示，正三棱柱ABC ? A1B1C1的各棱长均为2，其主视图如图所示，则此三棱柱左视图的面积为(　　)

    A．2 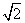B．4 C. D．2

    图K40?7

    　

    查看答案和解析>>

    同步练习册答案