练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知三棱锥S ­ ABC的三视图如图K38­1所示．在原三棱锥中给出下列结论：

    ①BC⊥平面SAC；②平面SBC⊥平面SAB；③SB⊥AC.

    其中，正确的结论是________(填序号)．


    ①


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图①所示,在直角三角形ABC中,∠ACB=30°,∠ABC=90°,D为AC的中点,E为BD的中点,AE的延长线交BC于点F,将△ABD沿BD折起,二面角ABDC的大小记为θ,如图②所示.

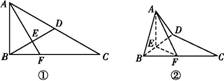
    (1)求证:平面AEF⊥平面BCD;

    (2)当cos θ为何值时,AB⊥CD.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    两圆相交于(1，3)和(m，－1)两点，两圆圆心都在直线x－y＋c＝0上，且m，c均为实数，则m＋c＝(　　)

    A．0  B．1

    C．2  D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数：

    ①sin213°＋cos217°－sin 13°cos 17°＝；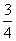

    ②sin215°＋cos215°－sin 15°cos 15°＝；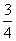

    ③sin218°＋cos212°－sin 18°cos 12°＝；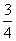

    ④sin2(－18°)＋cos248°－sin(－18°)cos 48°＝；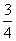

    ⑤sin2(－25°)＋cos255°－sin(－25°)cos 55°＝.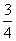

    将该同学的发现推广为三角恒等式：________________________________________________________________________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用反证法证明命题“若a，b∈N，ab能被3整除，那么a，b中至少有一个能被3整除”时，假设应为(　　)

    A．a，b都能被3整除 

    B．a，b都不能被3整除

    C．b不能被3整除 

    D．a不能被3整除

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用数学归纳法证明“n3＋(n＋1)3＋(n＋2)3(n∈N*)能被9整除”，要利用归纳假设证当n＝k＋1时的情况，只需展开(　　)

    A．(k＋3)3  B．(k＋2)3

    C．(k＋1)3  D．(k＋1)3＋(k＋2)3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用数学归纳法证明C＋C＋…＋C>n(n≥n0且n0∈N*)，则n的最小值为(　　)

    A．1  B．2  C．3  D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a，b，c为三条不同的直线，且a⊂平面α，b⊂平面β，α∩β＝c.给出下列命题：

    ①若a与b是异面直线，则c至少与a，b中的一条相交；

    ②若a不垂直于c，则a与b一定不垂直；

    ③若a∥b，则必有a∥c；

    ④若a⊥b，a⊥c，则必有α⊥β.

    其中真命题的个数是(　　)

    A．0  B．1 

    C．2  D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设m，n是两条不同的直线，α，β，γ是三个不同的平面，给出下列四个命题：①若m⊂β，α⊥β，则m⊥α；②若α∥β，m⊂α，则m∥β；③若n⊥α，n⊥β，m⊥α，则m⊥β；④若α⊥γ，β⊥γ，m⊥α，则m⊥β.其中真命题的序号是(　　)

    A．①③  B．①②

    C．③④  D．②③

    查看答案和解析>>

    同步练习册答案