
【题目】已知函数f(x)=|ax﹣1|﹣(a﹣1)x
(1)当a= ![]() 时,满足不等式f(x)>1的x的取值范围为;
时,满足不等式f(x)>1的x的取值范围为;
(2)若函数f(x)的图象与x轴没有交点,则实数a的取值范围为 .
【答案】
(1)(2,+∞)
(2)[ ![]() ,1)
,1)
【解析】解:(1)a= ![]() 时,f(x)=|
时,f(x)=| ![]() x﹣1|+
x﹣1|+ ![]() x=
x= ![]() ,
,
∵f(x)>1,
∴ ![]() ,
,
解得x>2,
故x的取值范围为(2,+∞),(2)函数f(x)的图象与x轴没有交点,
①当a≥1时,f(x)=|ax﹣1|与g(x)=(a﹣1)x的图象:

两函数的图象恒有交点,
②当0<a<1时,f(x)=|ax﹣1|与g(x)=(a﹣1)x的图象:

要使两个图象无交点,斜率满足:a﹣1≥﹣a,
∴a≥ ![]() ,故
,故 ![]() ≤≤a<1
≤≤a<1
③当a≤0时,f(x)=|ax﹣1|与g(x)=(a﹣1)x的图象:
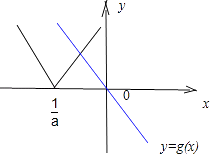
两函数的图象恒有交点,
综上①②③知: ![]() ≤a<1
≤a<1
故答案为:(2,+∞),[ ![]() ,1)
,1)
(1)化为分段函数,再解不等式即可,(2)①)当a≥1②当0<a<1③当a≤0三种情况,画出f(x)=|ax﹣1|与g(x)=(a﹣1)x的图象,利用图象确定有无交点.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示,下列说法正确的是( )
)的部分图象如图所示,下列说法正确的是( ) 
A.函数f(x)的图象关于直线x=﹣ ![]() 对称
对称
B.函数f(x)的图象关于点(﹣ ![]() ,0)对称
,0)对称
C.若方程f(x)=m在[﹣ ![]() ,0]上有两个不相等的实数根,则实数m∈(﹣2,﹣
,0]上有两个不相等的实数根,则实数m∈(﹣2,﹣ ![]() ]
]
D.将函数f(x)的图象向左平移 ![]() 个单位可得到一个偶函数
个单位可得到一个偶函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的右焦点F作该双曲线一条渐近线的垂线与两条渐近线相交于M,N两点,若|MN|=
=1(a>0,b>0)的右焦点F作该双曲线一条渐近线的垂线与两条渐近线相交于M,N两点,若|MN|= ![]() ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )
A.2或 ![]()
B.![]() 或
或 ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:x2+(y﹣4)2=4,点P是直线l:x﹣2y=0上的一动点,过点P作圆M的切线PA,PB,切点为A,B.
(1)当切线PA的长度为 ![]() 时,求点P的坐标;
时,求点P的坐标;
(2)若△PAM的外接圆为圆N,试问:当P在直线l上运动时,圆N是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由.
(3)求线段AB长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,A为以原点O为圆心的单位圆O与x正半轴的交点,在圆心角为 ![]() 的扇形AOB的弧AB上任取一点 P,作 PN⊥OA于N,连结PO,记∠PON=θ.
的扇形AOB的弧AB上任取一点 P,作 PN⊥OA于N,连结PO,记∠PON=θ. 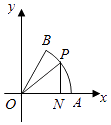
(1)设△PON的面积为y,使y取得最大值时的点P记为E,点N记为F,求此时 ![]() 的值;
的值;
(2)求k=a| ![]() ||
|| ![]() |+
|+ ![]() (a∈R,E 是在(1)条件下的点 E)的值域.
(a∈R,E 是在(1)条件下的点 E)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(﹣ ![]() ,0),B(
,0),B( ![]() ,0),锐角α的终边与单位圆O交于点P.
,0),锐角α的终边与单位圆O交于点P. 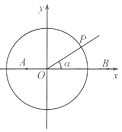
(Ⅰ)用α的三角函数表示点P的坐标;
(Ⅱ)当 ![]()
![]() =﹣
=﹣ ![]() 时,求α的值;
时,求α的值;
(Ⅲ)在x轴上是否存在定点M,使得| ![]() |=
|= ![]() |
| ![]() |恒成立?若存在,求出点M的横坐标;若不存在,请说明理由.
|恒成立?若存在,求出点M的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点P(2,3),根据下列条件分别求出直线l的方程:
(1)l在x轴、y轴上的截距之和等于0;
(2)l与两条坐标轴在第一象限所围城的三角形面积为16.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠BAD= ![]() ,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将ABE沿BE折起到A1BE的位置,如图2. (Ⅰ)证明:CD⊥平面A1OC;
,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将ABE沿BE折起到A1BE的位置,如图2. (Ⅰ)证明:CD⊥平面A1OC;
(Ⅱ)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某等腰三角形的底角为α,顶角为β,且cosβ= ![]() . (Ⅰ)求sinα的值;
. (Ⅰ)求sinα的值;
(Ⅱ)若函数f(x)=tanx在[﹣ ![]() ,α]上的值域与函数g(x)=2sin(2x﹣
,α]上的值域与函数g(x)=2sin(2x﹣ ![]() )在[0,m]上的值域相同,求m的取值范围.
)在[0,m]上的值域相同,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com