Question

【题目】如图，在平面直角坐标系中，点A（﹣ ，0），B（ ，0），锐角α的终边与单位圆O交于点P．
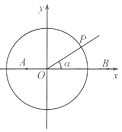
（Ⅰ）用α的三角函数表示点P的坐标；
（Ⅱ）当 =﹣ 时，求α的值；
（Ⅲ）在x轴上是否存在定点M，使得| |= | |恒成立？若存在，求出点M的横坐标；若不存在，请说明理由．

Answer 1

【答案】解：锐角α的终边与单位圆O交于点P．

（Ⅰ）用α的三角函数表示点P的坐标为（cosα，sinα）；

（Ⅱ） ， ， =﹣ 时，

即（cos ）（cos ）+sin2α= ，整理得到cos ，所以锐角α=60°；

（Ⅲ）在x轴上假设存在定点M，设M（x，0）， ，

则由| |= | |恒成立，得到 = ，整理得2cosα（2+x）=x2﹣4，

所以存在x=﹣2时等式恒成立，所以存在M（﹣2，0）．

【解析】（Ⅰ）用α的三角函数的坐标法定义得到P 坐标；（Ⅱ）首先写成两个向量的坐标根据 =﹣ ，得到关于α的三角函数等式，求α的值；（Ⅲ）假设存在M（x，0），进行向量的模长运算，得到三角等式，求得成立的x值．