
【题目】![]() =(3
=(3 ![]() sinx,
sinx, ![]() cosx),
cosx), ![]() =(cosx,
=(cosx, ![]() cosx),f (x)=
cosx),f (x)= ![]()
![]() .
.
(1)求f(x)的单调递减区间;
(2)x∈[﹣ ![]() ,
, ![]() ]时,g(x)=f(x)+m的最大值为
]时,g(x)=f(x)+m的最大值为 ![]() ,求g(x)的最小值及相应的x值.
,求g(x)的最小值及相应的x值.
【答案】
(1)解: ![]() =(3
=(3 ![]() sinx,
sinx, ![]() cosx),
cosx), ![]() =(cosx,
=(cosx, ![]() cosx),
cosx),
∴f (x)= ![]()
![]()
=3 ![]() sinxcosx+3cos2x
sinxcosx+3cos2x
= ![]() sin2x+
sin2x+ ![]()
=3sin(2x+ ![]() )+
)+ ![]() ;
;
令 ![]() +2kπ≤2x+
+2kπ≤2x+ ![]() ≤
≤ ![]() +2kπ,k∈Z,
+2kπ,k∈Z,
解得 ![]() +kπ≤x≤
+kπ≤x≤ ![]() +kπ,k∈Z,
+kπ,k∈Z,
∴f(x)的单调递减区间是[ ![]() +kπ,
+kπ, ![]() +kπ],k∈Z
+kπ],k∈Z
(2)解:x∈[﹣ ![]() ,
, ![]() ]时,2x+
]时,2x+ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
sin(2x+ ![]() )∈[﹣1,1],
)∈[﹣1,1],
∴3sin(2x+ ![]() )+
)+ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ];
];
∴f(x)的值域是[﹣ ![]() ,
, ![]() ],
],
∴g(x)=f(x)+m的最大值为 ![]() +m=
+m= ![]() ,
,
解得m=1,
∴g(x)=f(x)+1;
∴g(x)的最小值为﹣ ![]() +1=﹣
+1=﹣ ![]() ,
,
此时x=﹣ ![]() .
.
【解析】(1)根据平面向量的数量积计算并化简f (x),求出f(x)的单调递减区间;(2)根据x的取值范围,求出f(x)的值域,再根据g(x)的最大值求出m,从而求出g(x)的最小值与对应x的值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosxsin(x+ ![]() )﹣
)﹣ ![]() sin2x+sinxcosx.
sin2x+sinxcosx.
(1)当x∈[0, ![]() ]时,求f(x)的值域;
]时,求f(x)的值域;
(2)用五点法在图中作出y=f(x)在闭区间[﹣ ![]() ,
, ![]() ]上的简图;
]上的简图;
(3)说明f(x)的图象可由y=sinx的图象经过怎样的变化得到? 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知R(x0 , y0)是椭圆 ![]() +
+ ![]() =1上的一点,从原点O向圆R(x﹣x0)2+(y﹣y0)2=12作两条切线,分别交椭圆于P,Q两点.
=1上的一点,从原点O向圆R(x﹣x0)2+(y﹣y0)2=12作两条切线,分别交椭圆于P,Q两点. 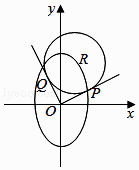
(1)若R点在第一象限,且直线OP,OQ互相垂直,求圆R的方程;
(2)若直线OP,OQ的斜率存在,分别记为k1 , k2 , 求k1k2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】矩形区域 ABCD 中,AB 长为 2 千米,BC 长为 1 千米,在 A 点和 C 点处各有一个通信基站,其覆盖范围均为方圆 1 千米,若在该矩形区域内随意选取一地点,则该地点无信号的概率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:x2+(y﹣4)2=4,点P是直线l:x﹣2y=0上的一动点,过点P作圆M的切线PA,PB,切点为A,B.
(1)当切线PA的长度为 ![]() 时,求点P的坐标;
时,求点P的坐标;
(2)若△PAM的外接圆为圆N,试问:当P在直线l上运动时,圆N是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由.
(3)求线段AB长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 其中M∪P=R,则下列结论中一定正确的是( )
其中M∪P=R,则下列结论中一定正确的是( )
A.函数f(x)一定存在最大值
B.函数f(x)一定存在最小值
C.函数f(x)一定不存在最大值
D.函数f(x)一定不存在最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(﹣ ![]() ,0),B(
,0),B( ![]() ,0),锐角α的终边与单位圆O交于点P.
,0),锐角α的终边与单位圆O交于点P. 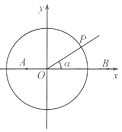
(Ⅰ)用α的三角函数表示点P的坐标;
(Ⅱ)当 ![]()
![]() =﹣
=﹣ ![]() 时,求α的值;
时,求α的值;
(Ⅲ)在x轴上是否存在定点M,使得| ![]() |=
|= ![]() |
| ![]() |恒成立?若存在,求出点M的横坐标;若不存在,请说明理由.
|恒成立?若存在,求出点M的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD边长为1,从某时刻起,将线段AB,BC,CD,DA分别绕点A,B,C,D顺时针旋转相同角度α(0<α< ![]() ),若旋转后的四条线段所围成的封闭图形面积为
),若旋转后的四条线段所围成的封闭图形面积为 ![]() ,则α=( )
,则α=( ) 
A.![]() 或
或 ![]()
B.![]() 或
或 ![]()
C.![]() 或
或 ![]()
D.![]() 或
或 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com