
【题目】已知函数 ![]() (a>0且a≠1)是奇函数.
(a>0且a≠1)是奇函数.
(1)求实数m的值;
(2)若1是函数y=f(x)+x的零点,求实数a的值.
【答案】
(1)解:因为函数f(x)为奇函数,则f(﹣x)+f(x)=0,即 ![]() ,
,
即 ![]() ,
,
所以 ![]() ,
,
故有m2=4,所以m=±2,
当m=﹣2时, ![]() =﹣1<0不成立,
=﹣1<0不成立,
当m=2时, ![]() ,经验证成立,
,经验证成立,
所以m=2
(2)解:由(1)知 ![]() ,
,
∵1是函数y=f(x)+x的零点,
∴f(1)+1=0,
即 ![]() ,
,
即loga3=1,
解得a=3
【解析】(1)根据奇函数满足f(-x)+f(x)=0列出方程解出m,并检验;(2)当x0是函数f(x)的零点时,f(x0)=0.
【考点精析】掌握函数奇偶性的性质和函数的零点与方程根的关系是解答本题的根本,需要知道在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇;二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点.


科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,AB=BC=1,AA1=2,E为BB1中点. (Ⅰ)证明:AC⊥D1E;
(Ⅱ)求DE与平面AD1E所成角的正弦值;
(Ⅲ)在棱AD上是否存在一点P,使得BP∥平面AD1E?若存在,求DP的长;若不存在,说明理由.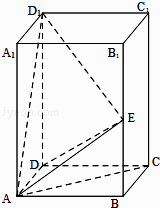
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() =(3
=(3 ![]() sinx,
sinx, ![]() cosx),
cosx), ![]() =(cosx,
=(cosx, ![]() cosx),f (x)=
cosx),f (x)= ![]()
![]() .
.
(1)求f(x)的单调递减区间;
(2)x∈[﹣ ![]() ,
, ![]() ]时,g(x)=f(x)+m的最大值为
]时,g(x)=f(x)+m的最大值为 ![]() ,求g(x)的最小值及相应的x值.
,求g(x)的最小值及相应的x值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家规定个人稿费纳税方法为:不超过800元的不纳税,超过800且不超过4000元的按超过800元的部分14%纳税,超过4000元的按全部稿费的11%纳税,
(1)试根据上述规定建立某人所得稿费x元与纳税额y元的函数关系;
(2)某人出了一本书,获得20000元的个人稿费,则这个人需要纳税是多少元?
(3)某人发表一篇文章共纳税70元,则这个人的稿费是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ax+b(a,b∈R). (Ⅰ)已知x∈[0,1]
(i)若a=b=1,求函数f(x)的值域;
(ii)若函数f(x)的值域为[0,1],求a,b的值;
(Ⅱ)当|x|≥2时,恒有f(x)≥0,且f(x)在区间(2,3]上的最大值为1,求a2+b2的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,过椭圆M: ![]() (a>b>0)右焦点的直线x+y﹣
(a>b>0)右焦点的直线x+y﹣ ![]() =0交M于A,B两点,P为AB的中点,且OP的斜率为
=0交M于A,B两点,P为AB的中点,且OP的斜率为 ![]() . (Ⅰ)求M的方程
. (Ⅰ)求M的方程
(Ⅱ)C,D为M上的两点,若四边形ACBD的对角线CD⊥AB,求四边形ACBD面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线x2+y=8与x轴交于A,B两点,动点P与A,B连线的斜率之积为 ![]() .
.
(1)求动点P的轨迹C的方程.
(2)MN是动点P轨迹C的一条弦,且直线OM,ON的斜率之积为 ![]() .求
.求 ![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com