Question

【题目】平面直角坐标系xOy中，过椭圆M： （a＞b＞0）右焦点的直线x+y﹣ =0交M于A，B两点，P为AB的中点，且OP的斜率为 ． （Ⅰ）求M的方程
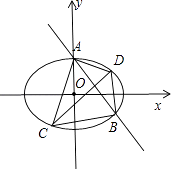
（Ⅱ）C，D为M上的两点，若四边形ACBD的对角线CD⊥AB，求四边形ACBD面积的最大值．

Answer 1

【答案】解：（Ⅰ）把右焦点（c，0）代入直线x+y﹣ =0得c+0﹣ =0，解得c= ． 设A（x1 ， y1），B（x2 ， y2），线段AB的中点P（x0 ， y0），
则 ， ，相减得 ，
∴ ，
∴ ，又 = ，
∴ ，即a2=2b2 ．
联立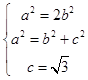得 ，解得 ，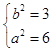
∴M的方程为 ．
（Ⅱ）∵CD⊥AB，∴可设直线CD的方程为y=x+t，
联立 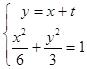，消去y得到3x2+4tx+2t2﹣6=0，
∵直线CD与椭圆有两个不同的交点，
∴△=16t2﹣12（2t2﹣6）=72﹣8t2＞0，解﹣3＜t＜3（*）．
设C（x3 ， y3），D（x4 ， y4），∴ ， ．
∴|CD|= = = ．
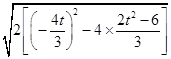联立 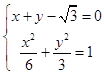得到3x2﹣4 x=0，解得x=0或 ，
∴交点为A（0， ），B ，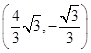
∴|AB|= = ．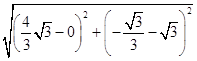
∴S四边形ACBD= = = ，
∴当且仅当t=0时，四边形ACBD面积的最大值为 ，满足（*）．
∴四边形ACBD面积的最大值为 ．

【解析】（Ⅰ）把右焦点（c，0）代入直线可解得c．设A（x1 ， y1），B（x2 ， y2），线段AB的中点P（x0 ， y0），利用“点差法”即可得到a，b的关系式，再与a2=b2+c2联立即可得到a，b，c．（Ⅱ）由CD⊥AB，可设直线CD的方程为y=x+t，与椭圆的方程联立得到根与系数的关系，即可得到弦长|CD|．把直线x+y﹣ =0与椭圆的方程联立得到根与系数的关系，即可得到弦长|AB|，利用S四边形ACBD= 即可得到关于t的表达式，利用二次函数的单调性即可得到其最大值．