
【题目】已知函数f(x)=x2+ax+b(a,b∈R). (Ⅰ)已知x∈[0,1]
(i)若a=b=1,求函数f(x)的值域;
(ii)若函数f(x)的值域为[0,1],求a,b的值;
(Ⅱ)当|x|≥2时,恒有f(x)≥0,且f(x)在区间(2,3]上的最大值为1,求a2+b2的最大值和最小值.
【答案】解:(Ⅰ)(i),由已知,得f(x)=x2+x+1=(x+ ![]() )2+
)2+ ![]() ,
,
又x∈[0,1],
∴f(x)∈[1,3],
∴函数f(x)的值域的值域为[1,3],
(ii)函数y=f(x)的对称轴方程为x=﹣ ![]()
①当﹣ ![]() ≤0时,即a≥0时,函数f(x)在[0,1]上单调性递增,可得
≤0时,即a≥0时,函数f(x)在[0,1]上单调性递增,可得 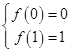 ,解得a=b=0,
,解得a=b=0,
②当﹣ ![]() ≥1时,即a≤﹣2时,函数f(x)在[0,1]上单调性递减,可得
≥1时,即a≤﹣2时,函数f(x)在[0,1]上单调性递减,可得  ,解得a=﹣2,b=1,
,解得a=﹣2,b=1,
③0<﹣ ![]() <
< ![]() 时,即﹣1<a<0时,
时,即﹣1<a<0时,
 ,解得a=﹣4,b=4,或a=b=0(舍去),
,解得a=﹣4,b=4,或a=b=0(舍去),
④当 ![]() ≤﹣
≤﹣ ![]() <1,即﹣2<a≤﹣1时,
<1,即﹣2<a≤﹣1时,  ,解得a=±2,b=1,舍去,
,解得a=±2,b=1,舍去,
综上所述a=b=0,或a=﹣2,b=1
(Ⅱ)由题意函数图象为开口向上的抛物线,且f(x)在区间(2,3]上的最大值只能在闭端点取得,
故有f(2)≤f(3)=1,从而a≥﹣5且b=﹣3a﹣8.
①若f(x)=0有实根,则△=a2﹣4b≥0,
在区间[﹣2,2]有 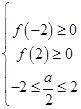 即
即  ,将b=3a﹣8代入,整理得
,将b=3a﹣8代入,整理得  即a=﹣4,这时b=4,且△=0.
即a=﹣4,这时b=4,且△=0.
②若f(x)=0无实根,则△=a2﹣4b<0,将b=﹣3a﹣8代入解得﹣8<a<﹣4.
综上﹣5≤a≤﹣4.
所以a2+b2=a2+(﹣3a﹣8)2=10a2+48a+64,在[﹣5,﹣4]单调递减,
故(a2+b2)min=32,(a2+b2)max=74.
【解析】(Ⅰ)(i)根据二次函数的性质即可求出函数的值域,(ii)根据二次函数的性质,分类讨论即可求出,(Ⅱ)因为若|x|≥2时,f(x)≥0,且f(x)在区间(2,3]上的最大值为1,f(x)在区间(2,3]上的最大值只能在闭端点取得,故有f(2)≤f(3)=1,从而a≥﹣5且b=﹣3a﹣8.在分类讨论基础上,将以上关系变为不等式组,消去c可得b的取值范围,最后将a2+b2转化为a的函数,求其值域可得a2+b2的最大值和最小值.
【考点精析】掌握二次函数在闭区间上的最值和二次函数的性质是解答本题的根本,需要知道当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() ;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知R(x0 , y0)是椭圆 ![]() +
+ ![]() =1上的一点,从原点O向圆R(x﹣x0)2+(y﹣y0)2=12作两条切线,分别交椭圆于P,Q两点.
=1上的一点,从原点O向圆R(x﹣x0)2+(y﹣y0)2=12作两条切线,分别交椭圆于P,Q两点. 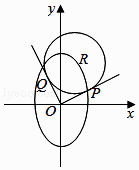
(1)若R点在第一象限,且直线OP,OQ互相垂直,求圆R的方程;
(2)若直线OP,OQ的斜率存在,分别记为k1 , k2 , 求k1k2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(﹣ ![]() ,0),B(
,0),B( ![]() ,0),锐角α的终边与单位圆O交于点P.
,0),锐角α的终边与单位圆O交于点P. 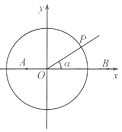
(Ⅰ)用α的三角函数表示点P的坐标;
(Ⅱ)当 ![]()
![]() =﹣
=﹣ ![]() 时,求α的值;
时,求α的值;
(Ⅲ)在x轴上是否存在定点M,使得| ![]() |=
|= ![]() |
| ![]() |恒成立?若存在,求出点M的横坐标;若不存在,请说明理由.
|恒成立?若存在,求出点M的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠BAD= ![]() ,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将ABE沿BE折起到A1BE的位置,如图2. (Ⅰ)证明:CD⊥平面A1OC;
,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将ABE沿BE折起到A1BE的位置,如图2. (Ⅰ)证明:CD⊥平面A1OC;
(Ⅱ)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知偶函数f(x)在[0,+∞)上是增函数,且f(1)=0,则满足f(log ![]() x)>0的x的取值范围是( )
x)>0的x的取值范围是( )
A.(0,+∞)
B.(0, ![]() )∪(2,+∞)
)∪(2,+∞)
C.(0, ![]() )
)
D.(0, ![]() )∪(1,2)
)∪(1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD边长为1,从某时刻起,将线段AB,BC,CD,DA分别绕点A,B,C,D顺时针旋转相同角度α(0<α< ![]() ),若旋转后的四条线段所围成的封闭图形面积为
),若旋转后的四条线段所围成的封闭图形面积为 ![]() ,则α=( )
,则α=( ) 
A.![]() 或
或 ![]()
B.![]() 或
或 ![]()
C.![]() 或
或 ![]()
D.![]() 或
或 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com