
【题目】已知曲线x2+y=8与x轴交于A,B两点,动点P与A,B连线的斜率之积为 ![]() .
.
(1)求动点P的轨迹C的方程.
(2)MN是动点P轨迹C的一条弦,且直线OM,ON的斜率之积为 ![]() .求
.求 ![]() 的最小值.
的最小值.
【答案】
(1)解:在方程x2+y=8中令y=0得:x=±2 ![]() ,
,
∴A(﹣2 ![]() ,0),B(2
,0),B(2 ![]() ,0).
,0).
设P(x,y),则kAPkBP= ![]() ,整理得:
,整理得: ![]() ,
,
动点P的轨迹C的方程为 ![]()
(2)解:设直线MN的方程为y=kx+m,M(x1,y1),N(x2,y2),
联立 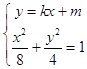 ,得(1+2k2)x2+4kmx+2m2﹣8=0,
,得(1+2k2)x2+4kmx+2m2﹣8=0,
∴x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
y1y2=(kx1+m)(kx2+m)=k2 ![]() +km
+km ![]() +m2=
+m2= ![]() ,
,
∵kOMkON=﹣ ![]() ,∴
,∴ ![]() ,即
,即 ![]() ,
,
得m2=4k2+2,
∴ ![]() =x1x2+y1y2=
=x1x2+y1y2= ![]() ,
,
∴﹣2≤ ![]() <2,
<2,
故 ![]() 的最小值为﹣2
的最小值为﹣2
【解析】(1)由已知曲线方程求出A,B的坐标,设P(x,y),结合kAPkBP= ![]() 列式求得动点P的轨迹C的方程;(2)设直线MN的方程为y=kx+m,M(x1 , y1),N(x2 , y2),联立直线方程与椭圆方程,由根与系数的关系结合直线OM,ON的斜率之积为
列式求得动点P的轨迹C的方程;(2)设直线MN的方程为y=kx+m,M(x1 , y1),N(x2 , y2),联立直线方程与椭圆方程,由根与系数的关系结合直线OM,ON的斜率之积为 ![]() 可得m与k的关系,进一步求出
可得m与k的关系,进一步求出 ![]() 的范围得答案.
的范围得答案.


科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD边长为1,从某时刻起,将线段AB,BC,CD,DA分别绕点A,B,C,D顺时针旋转相同角度α(0<α< ![]() ),若旋转后的四条线段所围成的封闭图形面积为
),若旋转后的四条线段所围成的封闭图形面积为 ![]() ,则α=( )
,则α=( ) 
A.![]() 或
或 ![]()
B.![]() 或
或 ![]()
C.![]() 或
或 ![]()
D.![]() 或
或 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班50人的一次竞赛成绩的频数分布如下:[60,70):3人,[70,80):16人,[80,90):24人,[90,100]:7人,利用各组区间中点值,可估计本次比赛该班的平均分为( )
A.56
B.68
C.78
D.82
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a为实数,p:点M(1,1)在圆(x+a)2+(y﹣a)2=4的内部; q:x∈R,都有x2+ax+1≥0.
(1)若p为真命题,求a的取值范围;
(2)若q为假命题,求a的取值范围;
(3)若“p且q”为假命题,且“p或q”为真命题,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图的茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x、y的值分别为( ) 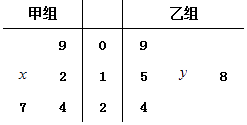
A.2,5
B.5,5
C.5,8
D.8,8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若圆的一条直径的两个端点分别是(﹣1,3)和(5,﹣5),则此圆的方程是( )
A.x2+y2+4x+2y﹣20=0
B.x2+y2﹣4x﹣2y﹣20=0
C.x2+y2﹣4x+2y+20=0
D.x2+y2﹣4x+2y﹣20=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AA1=AB=1,AD=2,E为BC的中点,点M,N分别为棱DD1 , A1D1的中点.
(1)求证:平面CMN∥平面A1DE;
(2)求证:平面A1DE⊥平面A1AE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com