
【题目】设某等腰三角形的底角为α,顶角为β,且cosβ= ![]() . (Ⅰ)求sinα的值;
. (Ⅰ)求sinα的值;
(Ⅱ)若函数f(x)=tanx在[﹣ ![]() ,α]上的值域与函数g(x)=2sin(2x﹣
,α]上的值域与函数g(x)=2sin(2x﹣ ![]() )在[0,m]上的值域相同,求m的取值范围.
)在[0,m]上的值域相同,求m的取值范围.
【答案】解:(Ⅰ)由题意,β=π﹣2α,
∴cosβ= ![]() =﹣cos2α=2sin2α﹣1
=﹣cos2α=2sin2α﹣1
∵α∈(0, ![]() ),∴sinα=
),∴sinα= ![]() ;
;
(Ⅱ)由题意,函数f(x)=tanx在[﹣ ![]() ,α]上单调递增,
,α]上单调递增,
∵α∈(0, ![]() ),sinα=
),sinα= ![]() ,∴cosα=
,∴cosα= ![]() ,∴tanα=2,
,∴tanα=2,
∴函数f(x)=tanx在[﹣ ![]() ,α]上的值域为[﹣
,α]上的值域为[﹣ ![]() ,2],
,2],
∴函数g(x)=2sin(2x﹣ ![]() )在[0,m]上的值域为[﹣
)在[0,m]上的值域为[﹣ ![]() ,2],
,2],
∴y=sinx在[﹣ ![]() ,2m﹣
,2m﹣ ![]() ]上的取值范围是[﹣
]上的取值范围是[﹣ ![]() ,1],
,1],
∴ ![]() ≤2m﹣
≤2m﹣ ![]() ≤
≤ ![]() ,
,
∴ ![]() ≤m≤
≤m≤ ![]() .
.
【解析】(Ⅰ)由题意,β=π﹣2α,利用cosβ= ![]() =﹣cos2α=2sin2α﹣1求sinα的值;(Ⅱ)若函数f(x)=tanx在[﹣
=﹣cos2α=2sin2α﹣1求sinα的值;(Ⅱ)若函数f(x)=tanx在[﹣ ![]() ,α]上的值域与函数g(x)=2sin(2x﹣
,α]上的值域与函数g(x)=2sin(2x﹣ ![]() )在[0,m]上的值域相同,得出y=sinx在[﹣
)在[0,m]上的值域相同,得出y=sinx在[﹣ ![]() ,2m﹣
,2m﹣ ![]() ]上的取值范围是[﹣
]上的取值范围是[﹣ ![]() ,1],即可求m的取值范围.
,1],即可求m的取值范围.
【考点精析】根据题目的已知条件,利用函数的值域的相关知识可以得到问题的答案,需要掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|ax﹣1|﹣(a﹣1)x
(1)当a= ![]() 时,满足不等式f(x)>1的x的取值范围为;
时,满足不等式f(x)>1的x的取值范围为;
(2)若函数f(x)的图象与x轴没有交点,则实数a的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知圆O:x2+y2=1,O1:(x﹣4)2+y2=4,动点P在直线x+ ![]() y+b=0上,过P分别作圆O,O1的切线,切点分别为A,B,若满足PB=2PA的点P有且只有两个,则实数b的取值范围是 .
y+b=0上,过P分别作圆O,O1的切线,切点分别为A,B,若满足PB=2PA的点P有且只有两个,则实数b的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知位于y轴左侧的圆C与y轴相切于点(0,1)且被x轴分成的两段圆弧长之比为1:2,过点H(0,t)的直线l于圆C相交于M、N两点,且以MN为直径的圆恰好经过坐标原点O. 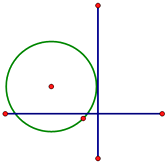
(1)求圆C的方程;
(2)当t=1时,求出直线l的方程;
(3)求直线OM的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式组 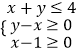 ,表示的平面区域为D,若圆C:(x+1)2+(y+1)2=r2(r>0)经过区域D上的点,则r的取值范围是( )
,表示的平面区域为D,若圆C:(x+1)2+(y+1)2=r2(r>0)经过区域D上的点,则r的取值范围是( )
A.[2 ![]() ,2
,2 ![]() ]
]
B.(2 ![]() ,3
,3 ![]() ]??
]??
C.(3 ![]() ,2
,2 ![]() ]
]
D.(0,2 ![]() )∪(2
)∪(2 ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线x2=4y,圆C:x2+(y﹣2)2=4,点M(x0 , y0),(x0>0,y0>4)为抛物线上的动点,过点M的圆C的两切线,设其斜率分别为k1 , k2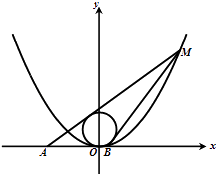
(Ⅰ)求证:k1+k2= ![]() ,k1k2=
,k1k2= ![]() .
.
(Ⅱ)求过点M的圆的两切线与x轴围成的三角形面积S的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com