练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设二次函数f(x)＝ax2－2ax＋c在区间[0,1]上单调递减，且f(m)≤f(0)，则实数m的取值范围是                                                                             (　　)

    A．(－∞，0]    B．[2，＋∞)   C．[0,2]   D．(－∞，0]∪[2，＋∞)


     C　二次函数f(x)＝ax2－2ax＋c在区间[0,1]上单调递减，则a≠0，f′(x)＝2a(x－1)<0，x∈[0,1]，所以a>0，即函数图象的开口向上，对称轴是直线x＝1.所以f(0)＝f(2)，则当f(m)≤f(0)时，有0≤m≤2.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知复数是纯虚数。            （1）求的值；

    （2）若复数，满足，求的最大值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


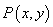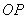    已知为函数图象上一点，O为坐标原点，记直线的斜率．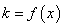

    （1）若函数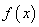在区间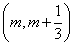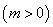上存在极值，求实数m的取值范围；

    （2）当 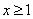时，不等式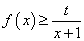恒成立，求实数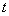的取值范围；

    （3）求证：．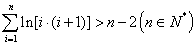

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一种十字绣作品由相同的小正方形构成，图①，②，③，④分别是制作该作品前四步时对应的图案，按照如此规律，第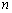步完成时对应图案中所包含小正方形的个数记为．

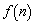    ①         ②          ③            ④

    （1）写出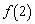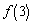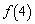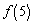，，，的值；

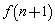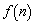    （2）利用归纳推理，归纳出与的关系式；

    （3）猜想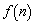的表达式，并写出推导过程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若一系列函数的解析式相同，值域相同，但定义域不同，则称这些函数为“同族函数”，则函数解析式为y＝x2＋1，值域为{1,3}的同族函数有(　　)

    A．1个       B．2个       C．3个      D．4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f＝lg x，则f(21)＝___________________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)，当x，y∈R时，恒有f(x＋y)＝f(x)＋f(y)．

    (1)求证：f(x)是奇函数；

    (2)如果x为正实数，f(x)<0，并且f(1)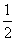＝－，试求f(x)在区间[－2,6]上的最值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    有下列几个命题：

    ①函数y =2x2+x+1在（0，＋∞）上是增函数；②函数y =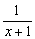在（－∞，－1）∪（－1，＋∞）上是减函数；③函数y =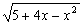的单调区间是［－2，+∞）；④已知f（x）在R上是增函数，若a+b＞0，则有f（a）+f（b）＞f（－a）+f（－b）.其中正确命题的序号是______________

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知复数满足．

    （1）求复数；（2）为何值时，复数对应点在第一象限．

    查看答案和解析>>

    同步练习册答案