
分析 (1)利用三角函数恒等变换的应用化简函数解析式可得f(x)=2$\sqrt{2}$sin($\frac{πx}{3}$+$\frac{π}{4}$)-2,根据三角函数周期公式即可求值得解;
(2)由x∈[$\frac{1}{4}$,$\frac{11}{4}$],可求$\frac{πx}{3}$+$\frac{π}{4}$∈[$\frac{π}{3}$,$\frac{7π}{6}$],利用正弦函数的图象和性质即可得解.
解答 (本题满分为13分)
解:(1)∵f(x)=2sin$\frac{πx}{3}$-4sin2$\frac{πx}{6}$
=2sin$\frac{πx}{3}$-2(1-cos$\frac{πx}{3}$)
=2$\sqrt{2}$(sin$\frac{πx}{3}$cos$\frac{π}{4}$+cos$\frac{πx}{3}$sin$\frac{π}{4}$)-2
=2$\sqrt{2}$sin($\frac{πx}{3}$+$\frac{π}{4}$)-2.…3分
∴f(x)的最小正周期T=$\frac{2π}{\frac{π}{3}}$=6.…5分
(2)∵x∈[$\frac{1}{4}$,$\frac{11}{4}$],
∴$\frac{πx}{3}$+$\frac{π}{4}$∈[$\frac{π}{3}$,$\frac{7π}{6}$],…7分
∵f(x)在区间[$\frac{1}{4}$,$\frac{3}{4}$]上是增函数,在区间[$\frac{3}{4}$,$\frac{11}{4}$]上是减函数,…9分
而f($\frac{1}{4}$)=$\sqrt{6}$-2,f($\frac{3}{4}$)=2$\sqrt{2}-2$,f($\frac{11}{4}$)=-$\sqrt{2}-2$,…11分
∴f(x)的区间[$\frac{1}{4}$,$\frac{11}{4}$]上的最大值为2$\sqrt{2}$-2,最小值为-$\sqrt{2}-2$.…13分
点评 本题主要考查了三角函数恒等变换的应用,正弦函数的图象和性质的应用,考查了数形结合思想和转化思想,属于中档题.


科目:高中数学 来源:2017届浙江嘉兴市高三上学期基础测试数学试卷(解析版) 题型:选择题
已知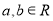 ,则“
,则“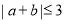 ”是“
”是“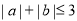 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
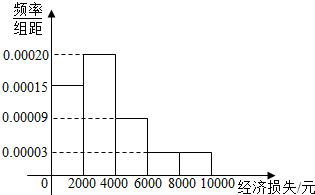 2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,给当地人民造成了巨大的财产损失,适逢暑假,小张调查了当地某小区的100户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(图1):
2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,给当地人民造成了巨大的财产损失,适逢暑假,小张调查了当地某小区的100户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(图1):| 经济损失不超过 4000元 | 经济损失超过 4000元 | 合计 | |
| 捐款超过 500元 | 60 | ||
| 捐款不超 过500元 | 10 | ||
| 合计 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{x}$)′=$\frac{1}{{x}^{2}}$ | B. | (log2x)′=$\frac{1}{xln2}$ | C. | (3x+1)′=x•3x-1+1 | D. | (cosx)′=sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com