
【题目】在如图所示的几何体中,四边形ABCD为正方形,![]() 为直角三角形,
为直角三角形,![]() ,且
,且![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)若AB=2AE,求异面直线BE与AC所成角的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)由已知可知AE⊥AB,又AE⊥AD,所以AE⊥平面ABCD,所以AE⊥DB,又ABCD为正方形,所以DB⊥AC,所以DB⊥平面AEC,而BD![]() 平面BED,故有平面AEC⊥平面BED.
平面BED,故有平面AEC⊥平面BED.
(2)作DE的中点F,连接OF,AF,由于O是DB的中点,且OF∥BE,可知∠FOA或其补角是异面直线BE与AC所成的角;设正方形ABCD的边长为2![]() ,则
,则![]() ,由于
,由于![]() ,AB=2AE,
,AB=2AE,
可知![]() ,
,![]() ,则
,则![]() ,又
,又![]() ,∴
,∴![]() =
=![]() ,由余弦定理的推理∴
,由余弦定理的推理∴![]() ∠FOA=
∠FOA=![]() =
=![]() ,故异面直线BE与AC所成的角的余弦值为
,故异面直线BE与AC所成的角的余弦值为![]() .
.
试题解析:(1)由已知有AE⊥AB,又AE⊥AD,
所以AE⊥平面ABCD,所以AE⊥DB, 3分
又ABCD为正方形,所以DB⊥AC, 4分
所以DB⊥平面AEC,BD![]() 面BED
面BED
故有平面AEC⊥平面BED. 6分
(2)作DE的中点F,连接OF,AF,
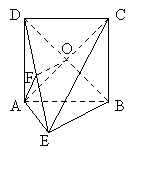
∵O是DB的中点,
∴OF∥BE,∴∠FOA或其补角是异面直线BE与AC所成的角。 8分
设正方形ABCD的边长为2![]() ,
,
则![]() , 9分
, 9分
∵![]() ,AB=2AE,
,AB=2AE,
∴![]() ,
,![]() ,∴
,∴![]() 10分
10分
又![]() ,∴
,∴![]() =
=![]() ,∴
,∴![]() ∠FOA=
∠FOA=![]() =
=![]()
∴异面直线BE与AC所成的角的余弦值为![]() 12分.
12分.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
【题目】莱市在市内主于道北京路一侧修建圆形休闲广场.如图,圆形广场的圆心为![]() ,半径为
,半径为![]() ,并与北京路一边所在直线
,并与北京路一边所在直线![]() 相切于点
相切于点![]() .点
.点![]() 为上半圆弧上一点,过点
为上半圆弧上一点,过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() .市园林局计划在
.市园林局计划在![]() 内进行绿化,设
内进行绿化,设![]() 的面积为
的面积为![]() (单位:
(单位:![]() ),
),![]() (单位:弧度).
(单位:弧度).

(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)当绿化面积![]() 最大时,试确定点
最大时,试确定点![]() 的位置,并求最大面积.
的位置,并求最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.某机构组织了一场诗词知识竞赛,将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,从中随机抽取100名选手进行调查,如图是根据调查结果绘制的选手等级与人数的条形图.
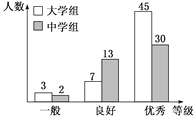
(1)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的2×2列联表,并据此判断能否在犯错误的概率不超过0.05的前提下认为选手成绩优秀与文化程度有关?
优秀 | 合格 | 总计 | |
大学组 | |||
中学组 | |||
总计 |
(2)若参赛选手共6万名,用频率估计概率,试估计其中优秀等级的选手人数;
(3)在优秀等级的选手中选取6名,在良好等级的选手中选取6名,都依次编号为1,2,3,4,5,6,在选出的6名优秀等级的选手中任取一名,记其编号为a,在选出的6名良好等级的选手中任取一名,记其编号为b,求使得方程组![]() 有唯一一组实数解(x,y)的概率.
有唯一一组实数解(x,y)的概率.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
P(K2≥k0) | 0.10 | 0.05 | 0.01 |
k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50名学生组成一个样本,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ……,第五组
……,第五组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.

(1)请估计学校1800名学生中,成绩属于第四组的人数;
(2)若成绩小于15秒认为良好,求该样本中在这次百米测试中成绩良好的人数;
(3)请根据频率分布直方图,求样本数据的众数、平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究学生的数学核素养与抽象(能力指标![]() )、推理(能力指标
)、推理(能力指标![]() )、建模(能力指标
)、建模(能力指标![]() )的相关性,并将它们各自量化为1、2、3三个等级,再用综合指标
)的相关性,并将它们各自量化为1、2、3三个等级,再用综合指标![]() 的值评定学生的数学核心素养,若
的值评定学生的数学核心素养,若![]() ,则数学核心素养为一级;若
,则数学核心素养为一级;若![]() ,则数学核心素养为二级;若
,则数学核心素养为二级;若![]() ,则数学核心素养为三级,为了了解某校学生的数学核素养,调查人员随机访问了某校10名学生,得到如下:
,则数学核心素养为三级,为了了解某校学生的数学核素养,调查人员随机访问了某校10名学生,得到如下:

(1)在这10名学生中任取两人,求这两人的建模能力指标相同的概率;
(2)从数学核心素养等级是一级的学生中任取一人,其综合指标为![]() ,从数学核心素养等级不是一级的学生中任取一人,其综合指标为
,从数学核心素养等级不是一级的学生中任取一人,其综合指标为![]() ,记随机变量
,记随机变量![]() ,求随机变量
,求随机变量![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产一种产品,质量测试分为:指标不小于90为一等品,不小于80小于90为二等品,小于80为三等品,每件一等品盈利50元,每件二等品盈利30元,每件三等品亏损10元.现对学徒工甲和正式工人乙生产的产品各100件的检测结果统计如下:

根据上表统计得到甲、乙生产产品等级的频率分别估计为他们生产产品等级的概率.
(Ⅰ)求出甲生产三等品的概率;
(Ⅱ)求出乙生产一件产品,盈利不小于30元的概率;
(Ⅲ)若甲、乙一天生产产品分别为30件和40件,估计甲、乙两人一天共为企业创收多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com