Question

【题目】在梯形ABCD中，DC∥AB，DC⊥CB，E是AB的中点，且AB=2BC=2CD=4（如图所示），将△ADE沿DE翻折，使AB=2（如图所示），F是线段AD上一点，且AF=2DF．

（Ⅰ）求四棱锥A-BCDE的体积；

（Ⅱ）在线段BE上是否存在一点G，使EF∥平面ACG？若存在，请指出点G的位置，并证明你的结论；若不存在，请说明理由．

Answer 1

【答案】（Ⅰ）（Ⅱ）线段BE上存在一点G，G是BE上靠近点B的三等分点，使EF∥平面ACG．

【解析】

（Ⅰ）取BE中点O，连结AO，证明AO⊥平面BCDE，即可计算四棱锥A-BCDE的体积。

（Ⅱ）过F作FH∥DC，交AC于H，在EB上取EG=FH，连结GH，证明FHEG，即可证明EF∥，问题得解。

解：（Ⅰ）∵在梯形ABCD中，DC∥AB，DC⊥CB，E是AB的中点，AB=2BC=2CD=4（如图1所示），

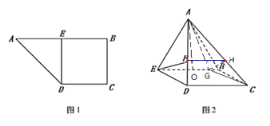
将△ADE沿DE翻折，使AB=2（如图2所示），

,∴平面ABE⊥

∴平面ABE⊥平面BCDE，四边形BCDE是以2为边长的正方形，

取BE中点O，连结AO，则AO⊥BE，

∴AO⊥平面BCDE，且AO==，

∴四棱锥A-BCDE的体积V===．

（Ⅱ）过F作FH∥DC，交AC于H，在EB上取EG=FH，连结GH，

∵F是线段AD上一点，且AF=2DF．

,

∴EG=2GB，即G是BE上靠近点B的三等分点，

此时，FHEG，∴四边形GEFH是平行四边形，∴EF∥GH，

∵EF平面ACG，GH平面ACG，

∴线段BE上存在一点G，G是BE上靠近点B的三等分点，使EF∥平面ACG．