
【题目】在![]() 中,D,E,F分别是边
中,D,E,F分别是边![]() ,
,![]() ,
,![]() 中点,下列说法正确的是( )
中点,下列说法正确的是( )
A.![]()
B.![]()
C.若 ,则
,则![]() 是
是![]() 在
在![]() 的投影向量
的投影向量
D.若点P是线段![]() 上的动点,且满足
上的动点,且满足![]() ,则
,则![]() 的最大值为
的最大值为![]()
【答案】BCD
【解析】
对选项A,B,利用平面向量的加减法即可判断A错误,B正确.对选项C,首先根据已知得到![]() 为
为![]() 的平分线,即
的平分线,即![]() ,再利用平面向量的投影概念即可判断C正确.对选项D,首先根据
,再利用平面向量的投影概念即可判断C正确.对选项D,首先根据![]() 三点共线,设
三点共线,设![]() ,
,![]() ,再根据已知得到
,再根据已知得到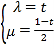 ,从而得到
,从而得到![]() ,即可判断选项D正确.
,即可判断选项D正确.
如图所示:
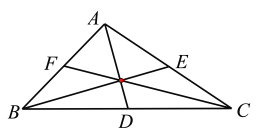
对选项A,![]() ,故A错误.
,故A错误.
对选项B,![]()
![]()
![]() ,故B正确.
,故B正确.
对选项C,![]() ,
,![]() ,
,![]() 分别表示平行于
分别表示平行于![]() ,
,![]() ,
,![]() 的单位向量,
的单位向量,
由平面向量加法可知:![]() 为
为![]() 的平分线表示的向量.
的平分线表示的向量.
因为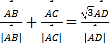 ,所以
,所以![]() 为
为![]() 的平分线,
的平分线,
又因为![]() 为
为![]() 的中线,所以
的中线,所以![]() ,如图所示:
,如图所示:

![]() 在
在![]() 的投影为
的投影为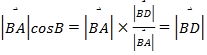 ,
,
所以![]() 是
是![]() 在
在![]() 的投影向量,故选项C正确.
的投影向量,故选项C正确.
对选项D,如图所示:
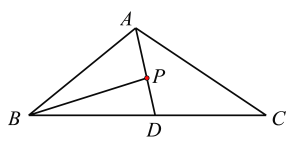
因为![]() 在
在![]() 上,即
上,即![]() 三点共线,
三点共线,
设![]() ,
,![]() .
.
又因为![]() ,所以
,所以![]() .
.
因为![]() ,则
,则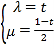 ,
,![]() .
.
令![]() ,
,
当![]() 时,
时,![]() 取得最大值为
取得最大值为![]() .故选项D正确.
.故选项D正确.
故选:BCD


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱![]() 中,所有棱长都等于
中,所有棱长都等于![]() .
.

(1)当点![]() 是
是![]() 的中点时,
的中点时,
①求异面直线![]() 和
和![]() 所成角的余弦值;
所成角的余弦值;
②求二面角![]() 的正弦值;
的正弦值;
(2)当点![]() 在线段
在线段![]() 上(包括两个端点)运动时,求直线
上(包括两个端点)运动时,求直线![]() 与平面
与平面![]() 所成角的正弦值的取值范围.
所成角的正弦值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某自行车手从O点出发,沿折线O﹣A﹣B﹣O匀速骑行,其中点A位于点O南偏东45°且与点O相距20 ![]() 千米.该车手于上午8点整到达点A,8点20分骑至点C,其中点C位于点O南偏东(45°﹣α)(其中sinα=
千米.该车手于上午8点整到达点A,8点20分骑至点C,其中点C位于点O南偏东(45°﹣α)(其中sinα= ![]() ,0°<α<90°)且与点O相距5
,0°<α<90°)且与点O相距5 ![]() 千米(假设所有路面及观测点都在同一水平面上).
千米(假设所有路面及观测点都在同一水平面上).
(1)求该自行车手的骑行速度;
(2)若点O正西方向27.5千米处有个气象观测站E,假定以点E为中心的3.5千米范围内有长时间的持续强降雨.试问:该自行车手会不会进入降雨区,并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知四棱锥![]() 的底面
的底面![]() 为矩形,
为矩形, ![]() 底面
底面![]() ,且
,且![]() (
(![]() ),
),![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.

(1)当![]() 为何值时,平面
为何值时,平面![]() 平面
平面![]() ?并证明你的结论;
?并证明你的结论;
(2)当异面直线![]() 与
与![]() 所成角的正切值为2时,求三棱锥
所成角的正切值为2时,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在梯形ABCD中,DC∥AB,DC⊥CB,E是AB的中点,且AB=2BC=2CD=4(如图所示),将△ADE沿DE翻折,使AB=2(如图所示),F是线段AD上一点,且AF=2DF.
(Ⅰ)求四棱锥A-BCDE的体积;
(Ⅱ)在线段BE上是否存在一点G,使EF∥平面ACG?若存在,请指出点G的位置,并证明你的结论;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:
①sin213°+cos217°﹣sin13°cos17°;
②sin215°+cos215°﹣sin15°cos15°;
③sin218°+cos212°﹣sin18°cos12°;
④sin2(﹣18°)+cos248°﹣sin(﹣18°)cos48°
⑤sin2(﹣25°)+cos255°﹣sin(﹣25°)cos55°
(Ⅰ)试从上述五个式子中选择一个,求出这个常数;
(Ⅱ)根据(Ⅰ)的计算结果,将该同学的发现推广为一三角恒等式sin2α+cos2(30°﹣α)﹣sinαcos(30°﹣α)= ,并证明你的结论.
(参考公式:sin(α±β)=sinαcosβ±cosαsinβ,cos(α±β)=cosαcosβsinαsinβsin2α=2sinαcosα,cos2α=cos2α﹣sin2α=2cos2α﹣1=1﹣2sin2α)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求方程![]() 的解集;
的解集;
(2)若关于x的方程![]() 在
在![]() 上恒有解,求m的取值范围;
上恒有解,求m的取值范围;
(3)若不等式![]() 在
在![]() 上恒成立,求m的取值范围;
上恒成立,求m的取值范围;
(4)若关于x的方程![]() 在
在![]() 上有解,那么当m取某一确定值时,方程所有解的和记为
上有解,那么当m取某一确定值时,方程所有解的和记为![]() ,求
,求![]() 所有可能值及相应的m的取值范围.
所有可能值及相应的m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com