
【题目】已知四棱锥![]() ,底面
,底面![]() 为菱形,
为菱形,![]() ,
,![]() 为
为![]() 上的点,过
上的点,过![]() 的平面分别交
的平面分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,且
,且![]() 平面
平面![]() .
.
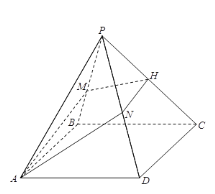
(1)证明:![]() ;
;
(2)当![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见证明(2) ![]()
【解析】
(1)连结![]() 、
、![]() 且
且![]() ,连结
,连结![]() ,先证明
,先证明![]() 平面
平面![]() ,可得
,可得![]() ,再利用线面平行的性质定理证明
,再利用线面平行的性质定理证明![]() ,从而可得结论;(2)利用(1)可证明
,从而可得结论;(2)利用(1)可证明![]() 平面
平面![]() ,利用
,利用![]() 与平面
与平面![]() 所成的角为
所成的角为![]() 求出线段间的等量关系,以
求出线段间的等量关系,以![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系,求出
轴,建立空间直角坐标系,求出![]() ,再利用向量垂直数量积为零列方程求出平面
,再利用向量垂直数量积为零列方程求出平面![]() 的法向量,由空间向量夹角余弦公式可得结果.
的法向量,由空间向量夹角余弦公式可得结果.
(1)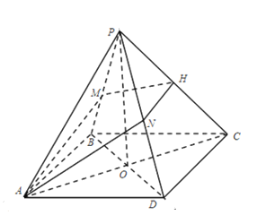
连结![]() 、
、![]() 且
且![]() ,连结
,连结![]() .
.
因为,![]() 为菱形,所以,
为菱形,所以,![]() ,
,
因为,![]() ,所以,
,所以,![]() ,
,
因为,![]() 且
且![]() 、
、![]()
![]() 平面
平面![]() ,
,
所以,![]() 平面
平面![]() ,
,
因为,![]()
![]() 平面
平面![]() ,所以,
,所以,![]() ,
,
因为,![]() 平面
平面![]() ,
,
且平面![]() 平面
平面![]() ,
,
所以,![]() ,
,
所以,![]() .
.
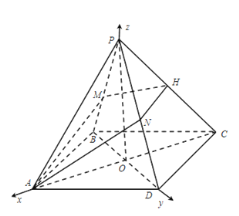
(2)
由(1)知![]() 且
且![]() ,
,
因为![]() ,且
,且![]() 为
为![]() 的中点,
的中点,
所以,![]() ,所以,
,所以,![]() 平面
平面![]() ,
,
所以![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,所以
,所以![]() ,
,
所以,![]() ,
,![]() ,因为,
,因为,![]() ,所以,
,所以,![]() .
.
以![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴,如图所示建立空间直角坐标系
轴,如图所示建立空间直角坐标系
记![]() ,所以,
,所以,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以, ![]() ,
,![]() ,
,![]()
记平面![]() 的法向量为
的法向量为![]() ,所以,
,所以,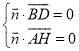 即
即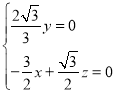 ,
,
令![]() ,解得
,解得![]() ,
,![]() ,所以,
,所以,![]() ,
,
记![]() 与平面
与平面![]() 所成角为
所成角为![]() ,所以,
,所以,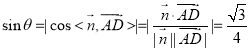 .
.
所以,![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 为曲线
为曲线![]() 上两点,
上两点,![]() 与
与![]() 的横坐标之和为
的横坐标之和为![]() .
.
(1)求直线![]() 的斜率;
的斜率;
(2)设弦![]() 的中点为
的中点为![]() ,过点
,过点![]() 、
、![]() 分别作抛物线的切线,则两切线的交点为
分别作抛物线的切线,则两切线的交点为![]() ,过点
,过点![]() 作直线
作直线![]() ,交抛物线于
,交抛物线于![]() 、
、![]() 两点,连接
两点,连接![]() 、
、![]() .证明:
.证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() (其中
(其中![]() )的部分图象如图所示,把函数
)的部分图象如图所示,把函数![]() 的图像向右平移
的图像向右平移![]() 个单位长度,再向下平移1个单位,得到函数
个单位长度,再向下平移1个单位,得到函数![]() 的图像.
的图像.

(1)当![]() 时,求
时,求![]() 的值域
的值域
(2)令![]() ,若对任意
,若对任意![]() 都有
都有![]() 恒成立,求
恒成立,求![]() 的最大值
的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为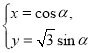 (
(![]() 为参数).以坐标原点为极点,以
为参数).以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,求
上,求![]() 的最小值及此时
的最小值及此时![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时.如图,某沙漏由上下两个圆锥组成,圆锥的底面直径和高均为8cm,细沙全部在上部时,其高度为圆锥高度的![]() (细管长度忽略不计).假设该沙漏每秒钟漏下
(细管长度忽略不计).假设该沙漏每秒钟漏下![]() 的沙,且细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆.以下结论正确的是( )
的沙,且细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆.以下结论正确的是( )
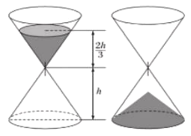
A.沙漏中的细沙体积为![]()
B.沙漏的体积是![]()
C.细沙全部漏入下部后此锥形沙堆的高度约为2.4cm
D.该沙漏的一个沙时大约是1985秒(![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() .
.
(1)求椭圆![]() 的方程,并求其离心率;
的方程,并求其离心率;
(2)过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,设点
,设点![]() 为第四象限内一点且在椭圆
为第四象限内一点且在椭圆![]() 上(点
上(点![]() 不在直线
不在直线![]() 上),点
上),点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,直线
,直线![]() 与
与![]() 交于另一点
交于另一点![]() .设
.设![]() 为原点,判断直线
为原点,判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由我国引领的5G时代已经到来,5G的发展将直接带动包括运营、制造、服务在内的通信行业整体的快速发展,进而对![]() 增长产生直接贡献,并通过产业间的关联效应和波及效应,间接带动国民经济各行业的发展,创造岀更多的经济增加值.如图是某单位结合近年数据,对今后几年的5G经济产出所做的预测.结合下图,下列说法正确的是( )
增长产生直接贡献,并通过产业间的关联效应和波及效应,间接带动国民经济各行业的发展,创造岀更多的经济增加值.如图是某单位结合近年数据,对今后几年的5G经济产出所做的预测.结合下图,下列说法正确的是( )
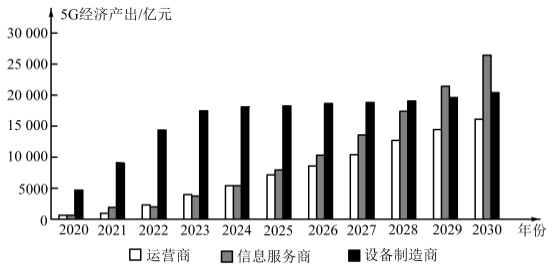
A.5G的发展带动今后几年的总经济产出逐年增加
B.设备制造商的经济产出前期增长较快,后期放缓
C.设备制造商在各年的总经济产出中一直处于领先地位
D.信息服务商与运营商的经济产出的差距有逐步拉大的趋势
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,以
两点,以![]() ,
,![]() 两点为切点分别作抛物线
两点为切点分别作抛物线![]() 的切线
的切线![]() ,
,![]() ,设
,设![]() 与
与![]() 交于点
交于点![]() .
.
(1)求![]() ;
;
(2)过![]() ,
,![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() ,
,![]() 两点,证明:
两点,证明:![]() ,并求四边形
,并求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com