
分析 a2+b2+c2+2ab-4a-4b+4=0,可得(a+b)2-4(a+b)+4+c2=0,即(a+b-2)2+c2=0,于是a+b=2,c=0.b>0.再利用导数研究函数的单调性即可得出.
解答 解:∵a2+b2+c2+2ab-4a-4b+4=0,∴(a+b)2-4(a+b)+4+c2=0,
∴(a+b-2)2+c2=0,
∴a+b=2,c=0.b=2-a>0.∴a<2,且a≠0.
∴$\frac{1}{2|a|}$+$\frac{|a|}{b}$+c=$\frac{1}{2|a|}$+$\frac{|a|}{b}$=$\frac{1}{2|a|}$+$\frac{|a|}{2-a}$=f(a),
①当0<a<2时,f(a)=$\frac{1}{2a}$+$\frac{a}{2-a}$=$\frac{1}{2a}$+$\frac{2}{2-a}$-1,f′(a)=$\frac{2}{(2-a)^{2}}$-$\frac{1}{2{a}^{2}}$=$\frac{3{a}^{2}+4a-4}{2{a}^{2}(2-a)^{2}}$=$\frac{(3a-2)(a+2)}{2{a}^{2}(2-a)^{2}}$,
可知:当a=$\frac{2}{3}$时,f(a)取得最小值,$f(\frac{2}{3})$=$\frac{5}{4}$.
②当a<0时,f(a)=$-\frac{1}{2a}$-$\frac{a}{2-a}$=-$\frac{1}{2a}$-$\frac{2}{2-a}$+1,f′(a)=-$\frac{2}{(2-a)^{2}}$+$\frac{1}{2{a}^{2}}$=-$\frac{3{a}^{2}+4a-4}{2{a}^{2}(2-a)^{2}}$=-$\frac{(3a-2)(a+2)}{2{a}^{2}(2-a)^{2}}$,
可知:当a=-2时,f(a)取得最小值,f(-2)=$\frac{3}{4}$.
综上可得:f(a)的最小值为:$\frac{3}{4}$.此时a=-2,b=4,c=0.
故答案为:$\frac{3}{4}$.
点评 本题考查了配方法、利用导数研究函数的单调性极值与最值,考查了分类讨论方法、推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
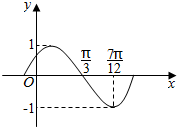 函数f(x)=sin(ωx+φ)(ω>0,|φ|>$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=sin(ωx+φ)(ω>0,|φ|>$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
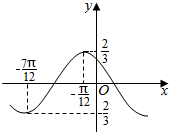 函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)图象的一段如图所示
函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)图象的一段如图所示查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,5) | B. | (-2,-5) | C. | (2,-5) | D. | (2,5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com