
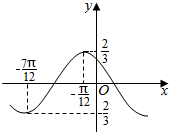
 函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)图象的一段如图所示
函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)图象的一段如图所示分析 (1)由图象可得A值,由周期公式可得ω,代点结合角的范围可得φ,可得解析式;
(2)由$0≤x≤\frac{π}{2}$和三角函数的最值可得.
解答 解:(1)由图象可得A=$\frac{2}{3}$,由$\frac{T}{2}$=-$\frac{π}{12}$-(-$\frac{7π}{12}$)=$\frac{π}{2}$可得周期T=π,
∴ω=$\frac{2π}{T}$=2,∴f(x)=$\frac{2}{3}$sin(2x+φ),
∵$f(x)=\frac{2}{3}sin(2x+φ)过点(-\frac{π}{12},\frac{2}{3})$,∴$sin(-\frac{π}{6}+φ)=1$
又0<φ<π,∴$-\frac{π}{6}<φ-\frac{π}{6}<\frac{5π}{6}$,故$φ-\frac{π}{6}=\frac{π}{2}$,可得$φ=\frac{2π}{3}$,
∴此函数的解析式为:$f(x)=\frac{2}{3}sin(2x+\frac{2π}{3})$;
(2)∵$0≤x≤\frac{π}{2}$,∴$\frac{2π}{3}≤2x+\frac{2π}{3}≤\frac{5π}{3}$,
∴f(x)在$2x+\frac{2π}{3}=\frac{2π}{3}$即x=0时取得最大值$f(0)=\frac{2}{3}sin\frac{2π}{3}=\frac{{\sqrt{3}}}{3}$,
f(x)在$2x+\frac{2π}{3}=\frac{3π}{2}$即$x=\frac{5π}{12}$时取得最小值$f(0)=\frac{2}{3}sin\frac{3π}{2}=-\frac{2}{3}$.
点评 本题考查三角函数的图象和解析式,涉及三角函数的最值,属中档题.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:填空题
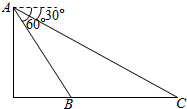 如图,从高为$200\sqrt{3}$米的气球(A)上测量铁桥(BC)的长,如果测得桥头B的俯角是60°,桥头C的俯角是30°,则桥BC长为400米.
如图,从高为$200\sqrt{3}$米的气球(A)上测量铁桥(BC)的长,如果测得桥头B的俯角是60°,桥头C的俯角是30°,则桥BC长为400米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
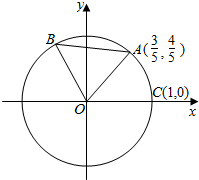 已知A、B是单位圆O上的点,且点B在第二象限,点C是圆O与x轴正半轴的交点,点A的坐标为$(\frac{3}{5},\frac{4}{5})$,若△AOB为正三角形.
已知A、B是单位圆O上的点,且点B在第二象限,点C是圆O与x轴正半轴的交点,点A的坐标为$(\frac{3}{5},\frac{4}{5})$,若△AOB为正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$] | B. | [-2,2] | C. | [-$\frac{\sqrt{2}}{2}$-1,$\frac{\sqrt{2}}{2}$] | D. | [-$\frac{\sqrt{2}}{2}$-1,$\frac{\sqrt{2}}{2}$+1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2-21-n | B. | 2n-1 | C. | 1 | D. | n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com