
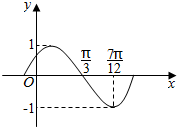
 函数f(x)=sin(ωx+φ)(ω>0,|φ|>$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=sin(ωx+φ)(ω>0,|φ|>$\frac{π}{2}$)的部分图象如图所示.分析 (1)由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
(2)由条件利用函数y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,再根据正弦函数的单调性,求得g(x)的单调递增区间.
解答 解:(1)由条件利用 函数f(x)=sin(ωx+φ)(ω>0,|φ|>$\frac{π}{2}$)的部分图象,
函数f(x)=sin(ωx+φ)(ω>0,|φ|>$\frac{π}{2}$)的部分图象,
易知:$\frac{T}{4}=\frac{7π}{12}-\frac{π}{3}=\frac{π}{4}$,可得:ω=2,
所以,f(x)=sin(2x+φ),由五点法作图可得2•$\frac{π}{3}$+φ=π,
求得$φ=\frac{π}{3}$,所以,$f(x)=sin({2x+\frac{π}{3}})$.
(2)将f(x)的图象先向右平移$\frac{π}{3}$个单位,
可得y=sin[2(x-$\frac{π}{3}$)+$\frac{π}{3}$]=sin(2x-$\frac{π}{3}$)的图象;
再将所得图象的点纵坐标不变,横坐标变为原来的$\frac{1}{2}$,
可得$g(x)=sin({4x-\frac{π}{3}})$ 的图象.
则由$4x-\frac{π}{3}∈({-\frac{π}{2}+2kπ,\frac{π}{2}+2kπ})$,
解得:$x∈({-\frac{π}{24}+\frac{kπ}{2},\frac{5π}{24}+\frac{kπ}{2}})$,
所以,g(x)的单调递增区间为$({-\frac{π}{24}+\frac{kπ}{2},\frac{5π}{24}+\frac{kπ}{2}}),k∈Z$.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由五点法作图求出φ的值,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 工艺扇面是中国书画一种常见的表现形式.某班级想用布料制作一面如图所示的扇面.已知扇面展开的中心角为120°,外圆半径为60cm,内圆半径为30cm.则制作这样一面扇面需要的布料为2826cm2(用数字作答,π取3.14).
工艺扇面是中国书画一种常见的表现形式.某班级想用布料制作一面如图所示的扇面.已知扇面展开的中心角为120°,外圆半径为60cm,内圆半径为30cm.则制作这样一面扇面需要的布料为2826cm2(用数字作答,π取3.14).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
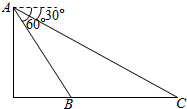 如图,从高为$200\sqrt{3}$米的气球(A)上测量铁桥(BC)的长,如果测得桥头B的俯角是60°,桥头C的俯角是30°,则桥BC长为400米.
如图,从高为$200\sqrt{3}$米的气球(A)上测量铁桥(BC)的长,如果测得桥头B的俯角是60°,桥头C的俯角是30°,则桥BC长为400米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2sin2x | B. | 2sin2x | C. | 2cos(2x-$\frac{π}{6}$) | D. | 2sin(2x-$\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com