函数y=sinx.x∈[0.2π]的图象与直线y=-$\frac{1}{2}$的交点有2个．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

10．函数y=sinx，x∈[0，2π]的图象与直线y=-$\frac{1}{2}$的交点有2个．

分析根据题意，在坐标系内作出函数y=sinx，x∈[0，2π]以及直线y=-$\frac{1}{2}$的图象，结合图象即可得出结论．

解答解：根据题意，在坐标系内作出函数y=sinx，x∈[0，2π]的简图，直线y=-$\frac{1}{2}$，
如图所示：

由数形结合可得，直线y=-$\frac{1}{2}$与y=sinx的图象有2个交点．
故答案为：2．

点评本题考查了正弦函数的图象与性质的应用问题，是基础题目．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

20．下列函数既是奇函数又在区间（0，+∞）上为增函数的是（　　）

A．

y=sinx，x∈R

B．

y=x²，x∈R

C．

y=x-$\frac{1}{x}$，x≠0

D．

y=2^-x，x∈R

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

1．

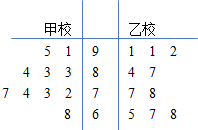为了解高一新生数学基础，甲、乙两校对高一新生进行了数学测试．现从两校各随机抽取10名新生的成绩作为样本，他们的测试成绩的茎叶图如下：
（1）比较甲、乙两校新生的数学测试样本成绩的平均值及方差的大小；（只需要写出结论）
（2）如果将数学基础采用A、B、C等级制，各等级对应的测试成绩标准如表：（满分100分，所有学生成绩均在60分以上）

测试成绩	[85，100]	[70，85）	（60，70）
基础等级	A	B	C

假设每个新生的测试成绩互相独立．根据所给数据，以事件发生的频率作为相应事件发生的概率．
从甲、乙两校新生中各随机抽取一名新生，求甲校新生的数学基础等级高于乙校新生的数学基础等级的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

18．

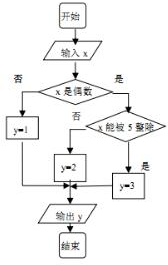某算法的程序图如图所示，其中输入的变量x在1，2，3，…，30这30个整数中等可能随机产生．
（1）分别求出按程序框图正确编程运行时输出y的值为i的概率P_i（i=1，2，3）；
（2）甲、乙两同学依据自己对程序框图的理解，各自编写程序重复运行n次后，统计记录了输出y的值为i（i=1，2，3）的频数，下面是甲、乙所作频数统计表的部分数据：
甲的频数统计表（部分）

运行次数	输出y=1的频数	输出y=2的频数	输出y=3的频数
50	24	19	7
…	…	…	…
2000	1027	776	197

乙的频数统计表（部分）

运行次数	输出y=1的频数	输出y=2的频数	输出y=3的频数
50	26	11	13
…	…	…	…
2000	1051	396	553

当n=2000时，根据表中的数据，分别写出甲、乙所编程序各自输出y的值为i（i=1，2，3）的频率（用分数表示），并判断甲、乙中谁所编写的程序符合算法要求的可能性较大．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

5．

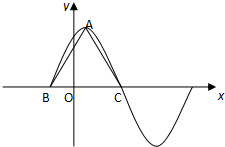已知f（x）=3cos²$\frac{ωx}{2}$+$\frac{\sqrt{3}}{2}$sinωx-$\frac{3}{2}$（ω＞0）在一个周期内的图象如图所示，点A为图象的最高点，B，C为图象与x轴的交点，且三角形ABC的面积为$\frac{\sqrt{3}}{4}$π．
（1）求ω的值及函数f（x）的对称轴方程；
（2）若f（x₀）=$\frac{4\sqrt{3}}{5}$，x₀∈（$\frac{π}{12}$，$\frac{π}{3}$），求f（x₀+$\frac{π}{6}$）的值．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

15．如果用$\overline{A}$表示随机事件A的对立事件，若事件A表示“汽车甲畅销且汽车乙滞销”，则事件$\overline{A}$表示（　　）