
【题目】已知圆![]() :
:![]() ,点
,点![]() .
.
(1)过点![]() 的直线
的直线![]() 与圆交与
与圆交与![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)从圆![]() 外一点
外一点![]() 向该圆引一条切线,切点记为
向该圆引一条切线,切点记为![]() ,
,![]() 为坐标原点,且满足
为坐标原点,且满足![]() ,求使得
,求使得![]() 取得最小值时点
取得最小值时点![]() 的坐标.
的坐标.
【答案】(1)![]() 或
或 ![]() (2)
(2)![]()
【解析】
试题分析:(1)⊙C:![]() ,化为标准方程,求出圆心C,半径r.分类讨论,利用C到l的距离为1,即可求直线l的方程;(2)设P(x,y).由切线的性质可得:CM⊥PM,利用|PM|=|PO|,可得y+x-1=0,求|PM|的最小值,即求|PO|的最小值,即求原点O到直线y+x-1=0的距离
,化为标准方程,求出圆心C,半径r.分类讨论,利用C到l的距离为1,即可求直线l的方程;(2)设P(x,y).由切线的性质可得:CM⊥PM,利用|PM|=|PO|,可得y+x-1=0,求|PM|的最小值,即求|PO|的最小值,即求原点O到直线y+x-1=0的距离
试题解析:圆![]() 方程可化为
方程可化为![]()
(1)当直线![]() 与
与![]() 轴垂直时,满足
轴垂直时,满足![]() ,所以此时
,所以此时![]()
当直线![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 方程为
方程为![]() ,
,
即![]()
因为![]() ,所以圆心到直线的距离
,所以圆心到直线的距离
![]()
由点到直线的距离公式得
![]() 解得
解得![]()
所以直线![]() 的方程为
的方程为
![]()
所以所求直线![]() 的方程为
的方程为![]() 或
或 ![]()
(2)因为![]() ,
,![]() ,
,![]()
化简得![]()
即点![]() 在直线
在直线![]() 上,
上,
当![]() 最小是时,即
最小是时,即![]() 取得最小,此时
取得最小,此时![]() 垂直直线
垂直直线![]()
所以![]() 的方程为
的方程为![]()
所以![]() 解得
解得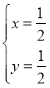
所以点![]() 的坐标为
的坐标为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
将圆![]() 上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线
上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线![]() .
.
(1)写出曲线![]() 的参数方程;
的参数方程;
(2)以坐标原点为极点,![]() 轴正半轴为极轴坐标建立极坐标系,已知直线
轴正半轴为极轴坐标建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,若
,若![]() 分别为曲线
分别为曲线![]() 和直线
和直线![]() 上的一点,求
上的一点,求![]() 的最近距离.
的最近距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,二次函数
,二次函数![]() ,关于
,关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,其中
,其中![]() 为非零常数,设
为非零常数,设![]() .
.
(1)求![]() 的值;
的值;
(2)若存在一条与![]() 轴垂直的直线和函数
轴垂直的直线和函数![]() 的图象相切,且切点的横坐标
的图象相切,且切点的横坐标![]() 满足
满足![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)当实数![]() 取何值时,函数
取何值时,函数![]() 存在极值?并求出相应的极值点.
存在极值?并求出相应的极值点.
查看答案和解析>>
科目:高中数学 来源: 题型:
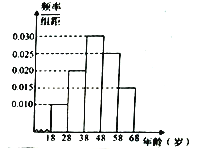
【题目】某地为弘扬中国传统文化举办“传统文化常识问答活动”,随机对该市![]() 岁的人群抽取一个容量为
岁的人群抽取一个容量为![]() 的样本,并将样本数据分成五组:
的样本,并将样本数据分成五组: ![]() ,再将其按从左到右的顺序分别编号为第
,再将其按从左到右的顺序分别编号为第![]() 组,第
组,第![]() 组,…,第
组,…,第![]() 组,绘制了样本的频率分布直方图,并对回答问题情况进行统计后,结果如下表所示.
组,绘制了样本的频率分布直方图,并对回答问题情况进行统计后,结果如下表所示.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的比例 |
第 | |
|
|
第 | |
|
|
第 | |
|
|
第 | |
|
|
第 | |
|
|
⑴分别求出![]() ,
, ![]() 的值;
的值;
⑵从![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,则第
人,则第![]() 组每组应各抽取多少人?
组每组应各抽取多少人?
⑶在⑵的前提下,决定在所抽取的![]() 人中随机抽取
人中随机抽取![]() 人颁发幸运奖,求所抽取的人中第
人颁发幸运奖,求所抽取的人中第![]() 组至少有
组至少有![]() 人获得幸运奖的概率.
人获得幸运奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与曲线
与曲线![]() 有三个不同的交点.
有三个不同的交点.
(1)求圆![]() 的方程;
的方程;
(2)已知点![]() 是
是![]() 轴上的动点,
轴上的动点, ![]() ,
, ![]() 分别切圆
分别切圆![]() 于
于![]() ,
, ![]() 两点.
两点.
①若![]() ,求
,求![]() 及直线
及直线![]() 的方程;
的方程;
②求证:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一河南旅游团到安徽旅游.看到安徽有很多特色食品,其中水果类较有名气的有:怀远石榴、砀山梨、徽州青枣等19种,点心类较有名气的有:一品玉带糕、徽墨酥、八公山大救驾等38种,小吃类较有名气的有:符离集烧鸡、无为熏鸭、合肥龙虾等57种.该旅游团的游客决定按分层抽样的方法从这些特产中买6种带给亲朋品尝.
(1)求应从水果类、点心类、小吃类中分别买回的种数;
(2)若某游客从买回的6种特产中随机抽取2种送给自己的父母,
①列出所有可能的抽取结果;
②求抽取的2种特产均为小吃的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是 ( )
A.由五个平面围成的多面体只能是四棱锥
B.棱锥的高线可能在几何体之外
C.仅有一组对面平行的六面体是棱台
D.有一个面是多边形,其余各面是三角形的几何体是棱锥
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com