
【题目】如图,在平面直角坐标系![]() 中,以
中,以![]() 轴正半轴为始边的锐角
轴正半轴为始边的锐角![]() 和钝角
和钝角![]() 的终边分别与单位圆交于点
的终边分别与单位圆交于点![]() ,若点
,若点![]() 的横坐标是
的横坐标是![]() ,点
,点![]() 的纵坐标是
的纵坐标是![]() .
.

(1)求![]() 的值;
的值;
(2)求![]() 的值.
的值.
【答案】(1)-![]() (2)
(2)![]()
【解析】
试题分析:(1)由任意角的三角函数的定义得cosα=![]() ,再根据同角三角函数关系及锐角范围求得sinα=
,再根据同角三角函数关系及锐角范围求得sinα=![]() =
=![]() .同理由任意角的三角函数的定义得sinβ=
.同理由任意角的三角函数的定义得sinβ=![]() ,再根据同角三角函数关系及锐角范围求得cosβ=-
,再根据同角三角函数关系及锐角范围求得cosβ=-![]() =-
=-![]() .最后根据两角差余弦公式得cos(α-β)=cosαcosβ+sinαsinβ
.最后根据两角差余弦公式得cos(α-β)=cosαcosβ+sinαsinβ
=![]() ×(-
×(-![]() )+
)+![]() ×
×![]() =-
=-![]() .(2)由于
.(2)由于![]() 的范围为(
的范围为(![]() ,
,![]() ),所以先求
),所以先求![]() 的正弦值:sin(α+β)=sinαcosβ+cosαsinβ=
的正弦值:sin(α+β)=sinαcosβ+cosαsinβ=![]() ×(-
×(-![]() )+
)+![]() ×
×![]() =
=![]() ,再根据正弦函数单调性确定
,再根据正弦函数单调性确定![]() 的值
的值
试题解析:因为锐角α的终边与单位圆交于A,且点A的横坐标是![]() ,
,
所以,由任意角的三角函数的定义可知,cosα=![]() ,
,
从而sinα=![]() =
=![]() .
.
因为钝角β的终边与单位圆交于点B,且点B的纵坐标是![]() ,
,
所以sinβ=![]() ,从而cosβ=-
,从而cosβ=-![]() =-
=-![]() .
.
(1)cos(α-β)=cosαcosβ+sinαsinβ
=![]() ×(-
×(-![]() )+
)+![]() ×
×![]() =-
=-![]() .
.
(2)sin(α+β)=sinαcosβ+cosαsinβ
=![]() ×(-
×(-![]() )+
)+![]() ×
×![]() =
=![]() .
.
因为α为锐角,β为钝角,故α+β∈(![]() ,
,![]() ),
),
所以α+β=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕的成本为50元,然后以每个100元的价格出售,如果当天卖不完,剩下的蛋糕作垃圾处理.现需决策此蛋糕店每天应该制作几个生日蛋糕,为此搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图所示的柱状图,以100天记录的各需求量的频率作为每天各需求量发生的概率.

(1)若蛋糕店一天制作17个生日蛋糕,
①求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:个,
(单位:个,![]() )的函数解析式;
)的函数解析式;
②在当天的利润不低于750元的条件下,求当天需求量不低于18个的概率.
(2)若蛋糕店计划一天制作16个或17个生日蛋糕,请你以蛋糕店一天利润的期望值为决定依据,判断应该制作16个是17个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 和定点
和定点![]() ,由圆
,由圆![]() 外一点
外一点![]() 向圆
向圆![]() 引切线
引切线![]() ,切点为
,切点为![]() ,且满足
,且满足![]() .
.

(1)求实数![]() 间满足的等量关系;
间满足的等量关系;
(2)若以![]() 为圆心的圆
为圆心的圆![]() 与圆
与圆![]() 有公共点,试求圆
有公共点,试求圆![]() 的半径最小时圆
的半径最小时圆![]() 的方程;
的方程;
(3)当![]() 点的位置发生变化时,直线
点的位置发生变化时,直线![]() 是否过定点,如果是,求出定点坐标,如果不是,说明理由.
是否过定点,如果是,求出定点坐标,如果不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(A)已知平行四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() .
.
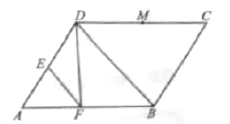
(1)求![]() 的长;
的长;
(2)设![]() ,
, ![]() 为线段
为线段![]() 、
、![]() 上的动点,且
上的动点,且![]() ,求
,求![]() 的最小值.
的最小值.
(B)已知平行四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() .
.
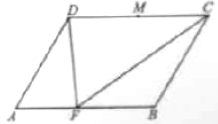
(1)求![]() 的长;
的长;
(2)设![]() 为线段
为线段![]() 上的动点(不包含端点),求
上的动点(不包含端点),求![]() 的最小值,以及此时点
的最小值,以及此时点![]() 的位置.
的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象关于直线
的图象关于直线![]() 对称,且图象上相邻最高点的距离为
对称,且图象上相邻最高点的距离为![]() .
.
⑴求![]() 的解析式;
的解析式;
⑵将![]() 的图象向右平移
的图象向右平移![]() 个单位,得到
个单位,得到![]() 的图象若关于
的图象若关于![]() 的方程
的方程![]() 在
在![]() 上有唯一解,求实数
上有唯一解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,点
,点![]() .
.
(1)过点![]() 的直线
的直线![]() 与圆交与
与圆交与![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)从圆![]() 外一点
外一点![]() 向该圆引一条切线,切点记为
向该圆引一条切线,切点记为![]() ,
,![]() 为坐标原点,且满足
为坐标原点,且满足![]() ,求使得
,求使得![]() 取得最小值时点
取得最小值时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() ,
,![]() ,且它的圆心在直线
,且它的圆心在直线![]() 上.
上.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)求圆![]() 关于直线
关于直线![]() 对称的圆的方程。
对称的圆的方程。
(Ⅲ)若点![]() 为圆
为圆![]() 上任意一点,且点
上任意一点,且点![]() ,求线段
,求线段![]() 的中点
的中点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知数列![]() 和
和![]() 满足
满足![]() ,若
,若![]() 为等比数列,且
为等比数列,且![]() ,
,![]() .
.
(1)求![]() 与
与![]() ;
;
(2)设![]() (
(![]() ),记数列
),记数列![]() 的前
的前![]() 项和为
项和为![]() ,
,
(I)求![]() ;
;
(II)求正整数![]() ,使得对任意
,使得对任意![]() 均有
均有![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com