
分析 (1)由题意可知:e=$\frac{c}{a}$=$\sqrt{\frac{{a}^{2}-{b}^{2}}{{a}^{2}}}$,求得3a2=4b2,根据点到直线的距离公式可知:$\frac{丨ab丨}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{2\sqrt{21}}{7}$,即可求得a和b的值,求得椭圆的方程;
(2)设直线方程为y=k(x+4),代入椭圆,求得${x_1}+{x_2}=\frac{{-32{k^2}}}{{3+4{k^2}}}$,${x_1}•{x_2}=\frac{{64{k^2}-12}}{{3+4{k^2}}}$,由向量的坐标表示.$\overrightarrow{MQ}$=λ$\overrightarrow{QN}$,求得$λ=-\frac{{{x_1}+4}}{{{x_2}+4}}$.,$\overrightarrow{MR}$=-λ$\overrightarrow{RN}$,代入即可求得R的横坐标.
解答 解:(1)由e=$\frac{c}{a}$=$\sqrt{\frac{{a}^{2}-{b}^{2}}{{a}^{2}}}$,
∴3a2=4b2,
由点到直线的距离公式可知:$\frac{丨ab丨}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{2\sqrt{21}}{7}$,
解得:$a=2,b=\sqrt{3}$,
∴椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
(2)直线MN的斜率必存在,设其直线方程为y=k(x+4),
并设M(x1,y1),M(x2,y2),联立方程$\left\{\begin{array}{l}\frac{x^2}{4}+\frac{y^2}{3}=1\\ y=k(x+4)\end{array}\right.$,
消去y得(3+4k2)x2+32k2x+64k-12=0,则△=144(1-4k2)>0,
由韦达定理可知:${x_1}+{x_2}=\frac{{-32{k^2}}}{{3+4{k^2}}}$,${x_1}•{x_2}=\frac{{64{k^2}-12}}{{3+4{k^2}}}$
由$\overrightarrow{MQ}=λ\overrightarrow{QN}$,得-4-x1=λ(x2+4),故$λ=-\frac{{{x_1}+4}}{{{x_2}+4}}$.
设点R的坐标为(x0,y0),则由$\overrightarrow{MR}=-λ•\overrightarrow{RN}$,得x0-x1=-λ(x2-x0),
解得:${x_0}=\frac{{{x_1}-λ{x_2}}}{1-λ}=\frac{{{x_1}+\frac{{{x_1}+4}}{{{x_2}+4}}•{x_2}}}{{1+\frac{{{x_1}+4}}{{{x_2}+4}}}}=\frac{{2{x_1}{x_2}+4({x_1}+{x_2})}}{{({x_1}+{x_2})+8}}$
又$2{x_1}{x_2}+4({x_1}+{x_2})=2×\frac{{64{k^2}-12}}{{3+4{k^2}}}+4×\frac{{-32{k^2}}}{{3+4{k^2}}}=\frac{-24}{{3+4{k^2}}}$,
$({x_1}+{x_2})+8=\frac{{-32{k^2}}}{{3+4{k^2}}}+8=\frac{24}{{3+4{k^2}}}$,从而${x_0}=\frac{{2{x_1}{x_2}+4({x_1}+{x_2})}}{{({x_1}+{x_2})+8}}=-1$,
故点R在定直线x=-1上.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,韦达定理,向量的坐标表示的综合应用,考查计算能力,属于中档题.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $±\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $±\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
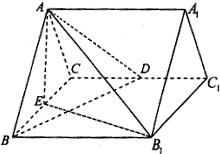 如图,已知正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点,E为BC的中点.
如图,已知正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点,E为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD=1,EC⊥BD,∠BCD=120°,EA=2,M是EC上的点,且EM=3MC.
如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD=1,EC⊥BD,∠BCD=120°,EA=2,M是EC上的点,且EM=3MC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com